Rotate a point about an arbitrary axis (3 dimensions)
Written by Paul Bourke
https://paulbourke.net/geometry/rotate/
/*
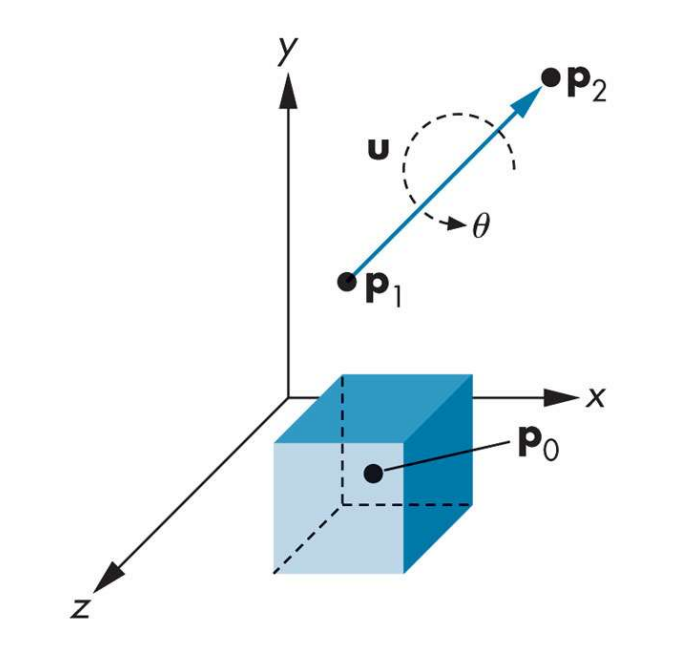
Rotate a point p by angle around an arbitrary line segment p1-p2
Return the rotated point.
Positive angles are anticlockwise looking down the axis
towards the origin. Assume right hand coordinate system.
*/
public static Vector3 ArbitraryRotate(Vector3 p, float angle, Vector3 p1, Vector3 p2)
{
Vector3 u, q1, q2, q3, q4, q5, q6, q7;
float d;
// (1) translate space so that the rotation axis passes through the origin
q1 = p – p1;
// (2) rotate space about the x axis so that the rotation axis lies in the xz plane
u = p2 – p1; // rotation-axis vector
u = Vector3.Normalize(u);
d = Mathf.Sqrt(u.y*u.y + u.z*u.z);
if (d != 0) {
q2.x = q1.x;
q2.y = q1.y * u.z / d – q1.z * u.y / d;
q2.z = q1.y * u.y / d + q1.z * u.z / d;
} else {
q2 = q1;
}
// (3) rotate space about the y axis so that the rotation axis lies along the z axis
q3.x = q2.x * d – q2.z * u.x;
q3.y = q2.y;
q3.z = q2.x * u.x + q2.z * d;
// (4) perform the desired rotation by theta about the z axis
float theta = Mathf.Deg2Rad * angle;
q4.x = q3.x * Mathf.Cos(theta) – q3.y * Mathf.Sin(theta);
q4.y = q3.x * Mathf.Sin(theta) + q3.y * Mathf.Cos(theta);
q4.z = q3.z;
// (5) apply the inverse of step (3)
q5.x = q4.x * d + q4.z * u.x;
q5.y = q4.y;
q5.z = -q4.x * u.x + q4.z * d;
// (6) apply the inverse of step (2)
if (d != 0) {
q6.x = q5.x;
q6.y = q5.y * u.z / d + q5.z * u.y / d;
q6.z = -q5.y * u.y / d + q5.z * u.z / d;
} else {
q6 = q5;
}
// (7) apply the inverse of step (1)
q7 = q6 + p1;
return q7;
}
/*
Rotate a point p by angle around an arbitrary axis
Return the rotated point.
Positive angles are anticlockwise looking down the axis
towards the origin. Assume right hand coordinate system.
*/
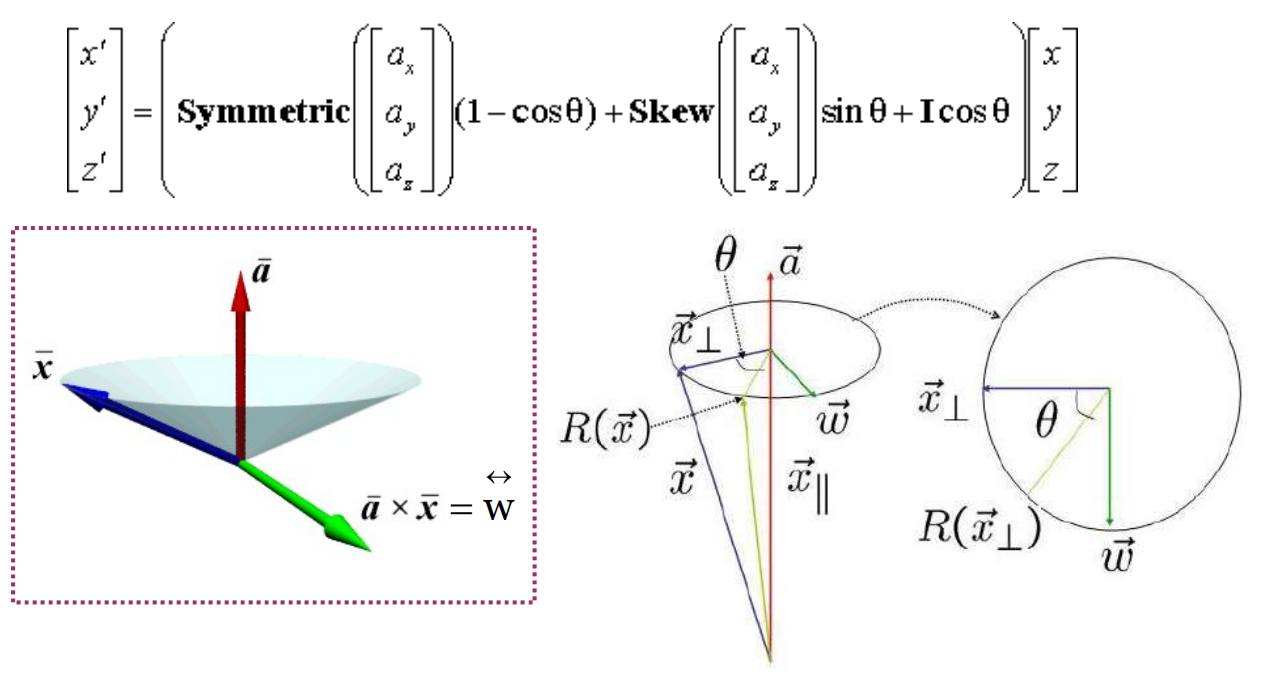
public static Vector3 ArbitraryRotate(Vector3 p, float angle, Vector3 axis)
{
Vector3 q = Vector3.zero;
float costheta, sintheta;
float theta = Mathf.Deg2Rad * angle;
axis = Vector3.Normalize(axis);
costheta = Mathf.Cos(theta);
sintheta = Mathf.Sin(theta);
q.x += (costheta + (1 – costheta) * axis.x * axis.x) * p.x;
q.x += ((1 – costheta) * axis.x * axis.y – axis.z * sintheta) * p.y;
q.x += ((1 – costheta) * axis.x * axis.z + axis.y * sintheta) * p.z;
q.y += ((1 – costheta) * axis.x * axis.y + axis.z * sintheta) * p.x;
q.y += (costheta + (1 – costheta) * axis.y * axis.y) * p.y;
q.y += ((1 – costheta) * axis.y * axis.z – axis.x * sintheta) * p.z;
q.z += ((1 – costheta) * axis.x * axis.z – axis.y * sintheta) * p.x;
q.z += ((1 – costheta) * axis.y * axis.z + axis.x * sintheta) * p.y;
q.z += (costheta + (1 – costheta) * axis.z * axis.z) * p.z;
return q;
}
