Computer Graphics 2025

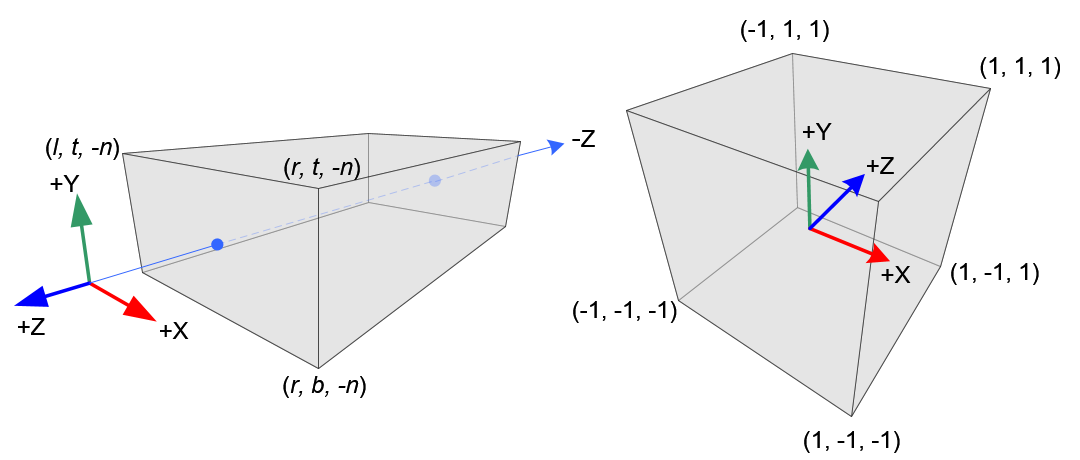
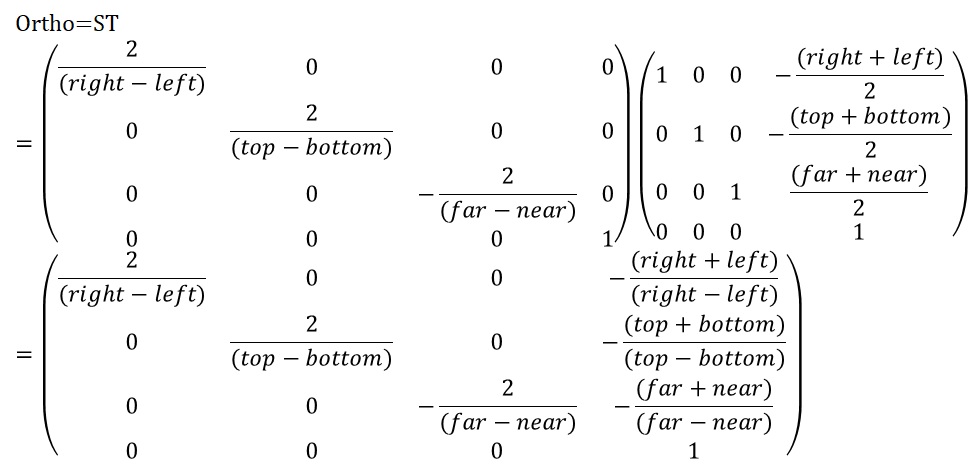
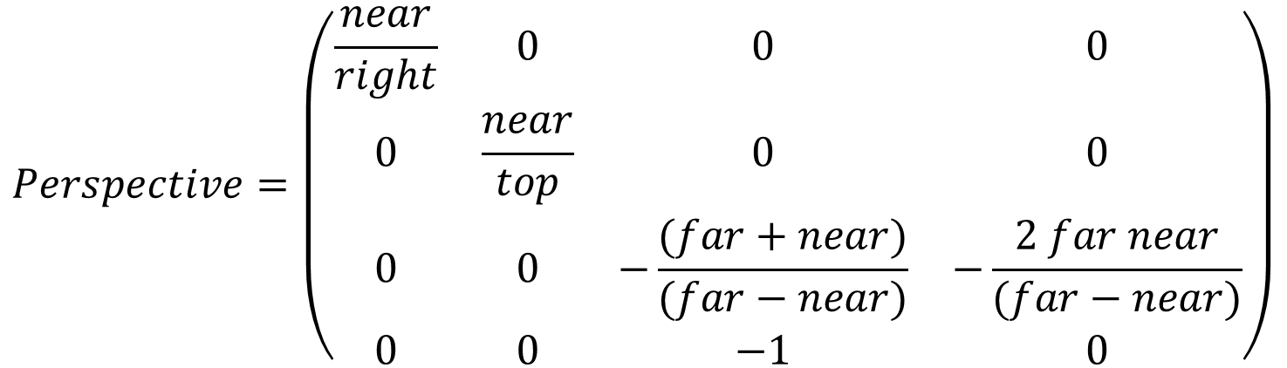Orthographic Projection

template <typename T>
 GLM_FUNC_QUALIFIER tmat4x4<T, defaultp> ortho
 (
  T left,
  T right,
  T bottom,
  T top,
  T zNear,
  T zFar
 )
 {
  tmat4x4<T, defaultp> Result(1);
  Result[0][0] = static_cast<T>(2) / (right - left);
  Result[1][1] = static_cast<T>(2) / (top - bottom);
  Result[2][2] = - static_cast<T>(2) / (zFar - zNear);
  Result[3][0] = - (right + left) / (right - left);
  Result[3][1] = - (top + bottom) / (top - bottom);
  Result[3][2] = - (zFar + zNear) / (zFar - zNear);
  return Result;
 }

Perspective Projection

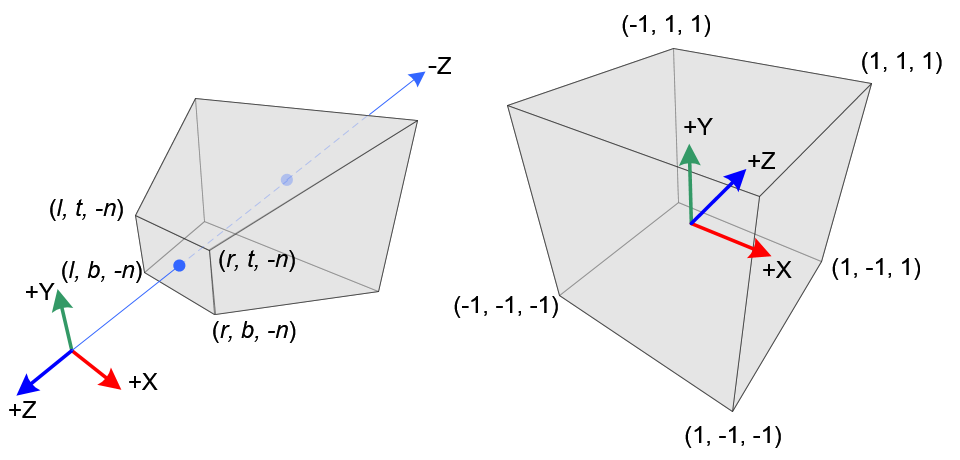
 template <typename T>
 GLM_FUNC_QUALIFIER tmat4x4<T, defaultp> frustum
 (
  T left,
  T right,
  T bottom,
  T top,
  T nearVal,
  T farVal
 )
 {
  tmat4x4<T, defaultp> Result(0);
  Result[0][0] = (static_cast<T>(2) * nearVal) / (right - left);
  Result[1][1] = (static_cast<T>(2) * nearVal) / (top - bottom);
  Result[2][0] = (right + left) / (right - left);
  Result[2][1] = (top + bottom) / (top - bottom);
  Result[2][2] = -(farVal + nearVal) / (farVal - nearVal);
  Result[2][3] = static_cast<T>(-1);
  Result[3][2] = -(static_cast<T>(2) * farVal * nearVal) / (farVal - nearVal);
  return Result;
 }

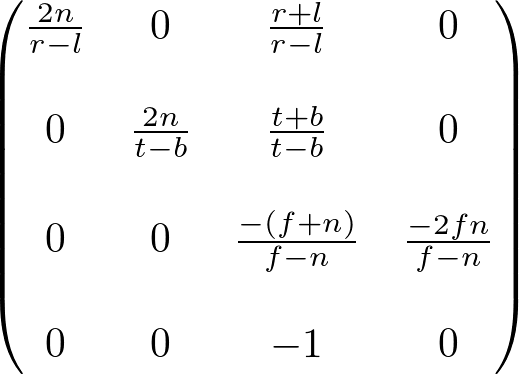
http://www.songho.ca/opengl/gl_projectionmatrix.html

mat4 projectionMatrix = glm::perspective (float fovy, float aspect, float near, float far) fovy radian

top = tan(fovy/2) * near

right = top * aspect

projectionMatrix = glm::frustum(-right, right, -top, top, near, far)

Matrix4x4.LookAt(Vector3 from, Vector4 to, Vector3 up) creates a “look at” matrix.

which is equal to Matrix4x4.TRS(from, Quaternion.LookRotation((to-from).normalized, up.normalized), Vector3.one)

Note that: glm::lookat != Matrix4x4.LookAt

template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAt(tvec3<T, P> const & eye, tvec3<T, P> const & center, tvec3<T, P> const & up)
{
# if GLM_COORDINATE_SYSTEM == GLM_LEFT_HANDED
return lookAtLH(eye, center, up);
# else
return lookAtRH(eye, center, up);
# endif
}

template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAtRH
(
tvec3<T, P> const & eye,
tvec3<T, P> const & center,
tvec3<T, P> const & up
)
{
tvec3<T, P> const f(normalize(center – eye));
tvec3<T, P> const s(normalize(cross(f, up)));
tvec3<T, P> const u(cross(s, f));

tmat4x4<T, P> Result(1);
Result[0][0] = s.x;
Result[1][0] = s.y;
Result[2][0] = s.z;
Result[0][1] = u.x;
Result[1][1] = u.y;
Result[2][1] = u.z;
Result[0][2] =-f.x;
Result[1][2] =-f.y;
Result[2][2] =-f.z;
Result[3][0] =-dot(s, eye);
Result[3][1] =-dot(u, eye);
Result[3][2] = dot(f, eye);
return Result;
}

template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAtLH
(
tvec3<T, P> const & eye,
tvec3<T, P> const & center,
tvec3<T, P> const & up
)
{
tvec3<T, P> const f(normalize(center – eye));
tvec3<T, P> const s(normalize(cross(up, f)));
tvec3<T, P> const u(cross(f, s));

tmat4x4<T, P> Result(1);
Result[0][0] = s.x;
Result[1][0] = s.y;
Result[2][0] = s.z;
Result[0][1] = u.x;
Result[1][1] = u.y;
Result[2][1] = u.z;
Result[0][2] = f.x;
Result[1][2] = f.y;
Result[2][2] = f.z;
Result[3][0] = -dot(s, eye);
Result[3][1] = -dot(u, eye);
Result[3][2] = -dot(f, eye);
return Result;
}

transform.LookAt()과 Quaternion.LookRotation()는 기능적으로 “오브젝트가 특정 방향(또는 목표 지점)을 바라보는 회전”을 정의한다는 점에서는 동일한 개념이나, transform.LookAt() 메서드는 오브젝트를 직접 지정한 위치와 방향으로 회전하는 반면, Quaternion.LookRotation() 메서드는 회전할 쿼터니언을 생성

Vector3 targetDir = target.position - transform.position;
Quaternion targetRot = Quaternion.LookRotation(targetDir);
transform.rotation = targetRot;

transform.LookAt(target);

void LookAt(Vector3 worldPosition, Vector3 worldUp = Vector3::up)
{
Vector3 forward = worldPosition - GetPosition();
Quaternion rot = Quaternion::LookRotation(forward, worldUp);
SetRotation(rot);
}

public static Quaternion LookRotation(Vector3 forward, [DefaultValue("Vector3.up")] Vector3 upwards)
{
return Quaternion.INTERNAL_CALL_LookRotation(ref forward, ref upwards);
}
[ExcludeFromDocs]
public static Quaternion LookRotation(Vector3 forward)
{
Vector3 up = Vector3.up;
return Quaternion.INTERNAL_CALL_LookRotation(ref forward, ref up);
}

// from http://answers.unity3d.com/questions/467614/what-is-the-source-code-of-quaternionlookrotation.html
private static Quaternion INTERNAL_CALL_LookRotation(ref Vector3 forward, ref Vector3 up)
{

forward = Vector3.Normalize(forward);
Vector3 right = Vector3.Normalize(Vector3.Cross(up, forward));
up = Vector3.Cross(forward, right);
var m00 = right.x;
var m01 = right.y;
var m02 = right.z;
var m10 = up.x;
var m11 = up.y;
var m12 = up.z;
var m20 = forward.x;
var m21 = forward.y;
var m22 = forward.z;

float num8 = (m00 + m11) + m22;
var quaternion = new Quaternion();
if (num8 > 0f)
{
var num = (float)Math.Sqrt(num8 + 1f);
quaternion.w = num * 0.5f;
num = 0.5f / num;
quaternion.x = (m12 - m21) * num;
quaternion.y = (m20 - m02) * num;
quaternion.z = (m01 - m10) * num;
return quaternion;
}
if ((m00 >= m11) && (m00 >= m22))
{
var num7 = (float)Math.Sqrt(((1f + m00) - m11) - m22);
var num4 = 0.5f / num7;
quaternion.x = 0.5f * num7;
quaternion.y = (m01 + m10) * num4;
quaternion.z = (m02 + m20) * num4;
quaternion.w = (m12 - m21) * num4;
return quaternion;
}
if (m11 > m22)
{
var num6 = (float)Math.Sqrt(((1f + m11) - m00) - m22);
var num3 = 0.5f / num6;
quaternion.x = (m10 + m01) * num3;
quaternion.y = 0.5f * num6;
quaternion.z = (m21 + m12) * num3;
quaternion.w = (m20 - m02) * num3;
return quaternion;
}
var num5 = (float)Math.Sqrt(((1f + m22) - m00) - m11);
var num2 = 0.5f / num5;
quaternion.x = (m20 + m02) * num2;
quaternion.y = (m21 + m12) * num2;
quaternion.z = 0.5f * num5;
quaternion.w = (m01 - m10) * num2;
return quaternion;
}

Images from https://en.wikipedia.org/wiki/Axonometric_projection

https://en.wikipedia.org/wiki/Gimbal_lock

How to Rotate in Unity (complete beginner’s guide)

// Create a Ra matrix Euler(30, 60, 45)
Matrix4x4 ra = Matrix4x4.Rotate(Quaternion.Euler(30, 60, 45));
// Create a Rb matrix rz -> rx -> ry
Matrix4x4 rz = Matrix4x4.Rotate(Quaternion.Euler(0, 0, 45));
Matrix4x4 rx = Matrix4x4.Rotate(Quaternion.Euler(30, 0, 0));
Matrix4x4 ry = Matrix4x4.Rotate(Quaternion.Euler(0, 60, 0));
Matrix4x4 rb = ry * rx * rz; // Z → X → Y

// ra == rb

// Create a Rc matrix ry -> rx -> rz
Matrix4x4 rc = rz * rx * ry; // Y → X → Z

// rb != rc