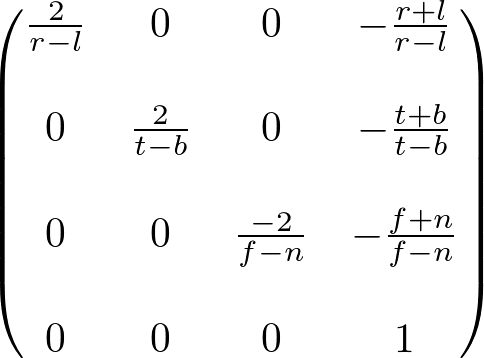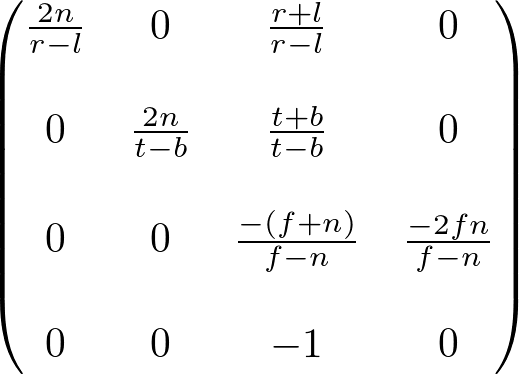강릉대 전자공학과
Monthly Archives: April 2014
Camera & View Matrix
 camera.cpp | camera.h |
F1&F2 – x축 카메라 위치이동
F3&F4 – y축 카메라 위치이동
F5&F6 – z축 카메라 위치이동
F7&F8 – x축 카메라 방향이동 (PITCH)
F9&F10 – y축 카메라 방향이동 (YAW)
HOME&END – z축 카메라 방향이동 (ROLL)
// main.cpp ——————————————
Camera camera1(FLY);
void init( void )
{
// 중간생략..
View = camera1.lookAt(g_eye, g_at, g_up);
}
void display( void )
{
// 중간생략..
View = camera1.View();
}
void specialkey(int key, int x, int y)
{
if (key == GLUT_KEY_F1) // x-movement
camera1.strafe(0.5);
else if (key == GLUT_KEY_F2)
camera1.strafe(-0.5);
else if (key == GLUT_KEY_F3) // y-movement
camera1.fly(0.5);
else if (key == GLUT_KEY_F4)
camera1.fly(-0.5);
else if (key == GLUT_KEY_F5) // z-movement
camera1.walk(0.5);
else if (key == GLUT_KEY_F6)
camera1.walk(-0.5);
else if (key == GLUT_KEY_F7) // yaw (by y-axis)
camera1.yaw(2.5);
else if (key == GLUT_KEY_F8)
camera1.yaw(-2.5);
else if (key == GLUT_KEY_F9) // pitch (by x-axis)
camera1.pitch(2.5);
else if (key == GLUT_KEY_F10)
camera1.pitch(-2.5);
else if (key == GLUT_KEY_HOME) // roll (by z-axis)
camera1.roll(2.5);
else if (key == GLUT_KEY_END)
camera1.roll(-2.5);
else if (key == GLUT_KEY_LEFT) // same as town
camera1.yaw(2.5);
else if (key == GLUT_KEY_RIGHT)
camera1.yaw(-2.5);
else if (key == GLUT_KEY_UP)
camera1.walk(0.5);
else if (key == GLUT_KEY_DOWN)
camera1.walk(-0.5);
glutPostRedisplay();
}
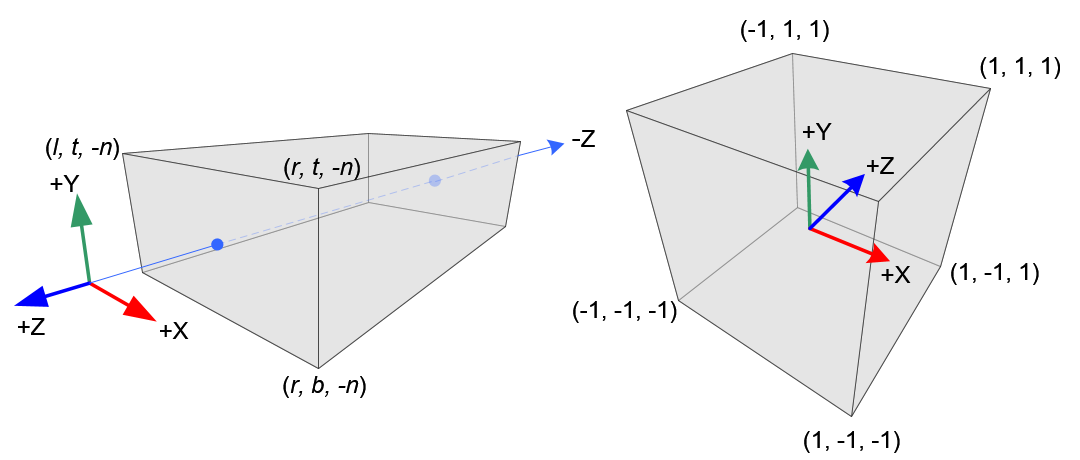
Projection Matrix
lecture12
lecture11
HW2
그래픽스 프로그래밍(321190) 실습 #2
– 3D graphics & hierarchical transformation & shading
(321190)
강사: 박경신
2014년 4월 24일
제출 방법: 2014년 5월 16일(금) 밤12시까지
(e-learning 강의실에 실행파일과 소스코드와 리포트를 전부 “학번이름_숙제2.zip”으로 묶어서 제출하도록 합니다. 또한, 소스코트 폴더에 .cpp만 담지 말고 비주얼 스튜디오에서 만든 프로젝트 폴더를 담기 바랍니다.) 9412924419.cpp1630232889.zip
참고자료: SimpleCar, SimpleSolar, SimpleMobile 등등
NOTE: 숙제 1의 기능을 활용해서 3차원 화를 한다.
0. Display window 크기는 1000 x 1000로 한다.
1. Hierarchical transformation 구조를 가진 ‘꽃/나무‘ 3종 이상을 만든다. (30점)
-Geometry 예제 (circle, cube, cylinder, sphere, square)와 Transformation 예제 (car, orbit, planet, robot, simple solar system)를 참고하여 본인만의 ‘꽃/나무 (내부 구성은 창의적으로)’를 구성하여 만든다.
-‘꽃/나무’에 사과, 배, 복숭아, 벚꽃 등등이 달려있다. (보고서에 스케치 첨부할 것)
-‘꽃/나무’ 물체는 적어도 3 단계 이상의 계층적 구조를 가진다. (움직임에 적용)
2. ‘Space bar’-key를 누르면 ‘꽃/나무’가 피어/자라난다. (20점)
-‘space bar’-key는 ‘꽃/나무’을 피어/자라나게 하는 button이다. 이 키를 다시 누르면 처음부터 다시 자라난다.
-움직이는 모드에서는 ‘꽃/나무’가 바람에 흔들리듯이 천천히 좌우로 움직이거나 회전을 한다. – 힌트: Idle() 함수를 사용할 것.
-가능하다면, 2단계 이상의 계층적 구조의 (즉, 부분적으로 다른) 움직임을 ‘꽃/나무’ 물체에 적용하도록 한다.
3. 메인 프로그램에서, 전체적인 장면에 조명과 재질을 사용하여 3차원 장면의 사실감을 더한다. (10점)
4. 창의성, 소스코드 주석처리, 리포트 (40점)
중간고사 답안
Hierarchical Transformation
Hierarchical Transformation
SimpleCar
SimpleRobot
SimpleSolar
//main.cpp ———————————————-
SimpleCar* car;
SimpleSolar* solar;
SimpleRobot* robot;
SimpleMobile* mobile;
void init()
{
// 중간생략
car = new SimpleCar();
robot = new SimpleRobot();
solar = new SimpleSolar();
mobile = new SimpleMobile();
}
void display()
{
// 중간생략
car->draw(&spMain, Projection, View, World);
robot->draw(&spMain, Projection, View, World);
solar->draw(&spMain, Projection, View, World);
mobile->draw(&spMain, Projection, View, World);
}
void update()
{
// 중간생략
car->update((float)deltaTime);
robot->update((float)deltaTime);
solar->update((float)deltaTime);
mobile->update((float)deltaTime);
glutPostRedisplay();
}
void specialkey(int key, int x, int y )
{
switch (key)
{
case GLUT_KEY_LEFT:
robot->setTheta(g_theta-=10.0f);
break;
case GLUT_KEY_RIGHT:
robot->setTheta(g_theta+=10.0f);
break;
// 중간생략
}
glutPostRedisplay();
}
OpenGL/GLM Transformation
// MVP matrix
Projection = glm::perspective(g_fovy, g_aspect, g_zNear, g_zFar);
View = glm::lookAt(g_eye, g_at, g_up);
spMain.useProgram();
spMain.setUniform(“gProjection”, Projection);
spMain.setUniform(“gView”, View);
// p’ = M3 * M2 * M1 * p (OpenGL uses Column-Major Order)
glm::mat4 Tx = glm::translate(glm::mat4(1.0f), glm::vec3(3.0f, 0.0f, 0.0f)); // RHS x+ right
glm::mat4 Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // RHS z+ (X->Y rotation)
glm::mat4 S = glm::scale(glm::mat4(1.0f), glm::vec3(0.5f, 0.7f, 1.0f)); // RHS
World = glm::mat4(1.0f);
spMain.setUniform(“gModel”, World);
cube1->draw();
// p’= R T p (red) => translate, and then rotate
glm::mat4 RT = Rz * Tx; // Translate X, and then Rotate Z
World = RT;
spMain.setUniform(“gModel”, World);
cube2->draw();
// p’= T R p (green) => rotate, and then translate
glm::mat4 TR = Tx * Rz; // Rotate Z, and then Translate X
World = TR;
spMain.setUniform(“gModel”, World);
cube3->draw();
// p’= T R S p (blue) => scale, and then rotate, and then translate
glm::mat4 TRS = Tx * Rz * S; // Scale XY, and then Rotate Z, and then Translate X
World = TRS;
spMain.setUniform(“gModel”, World);
cube4->draw();
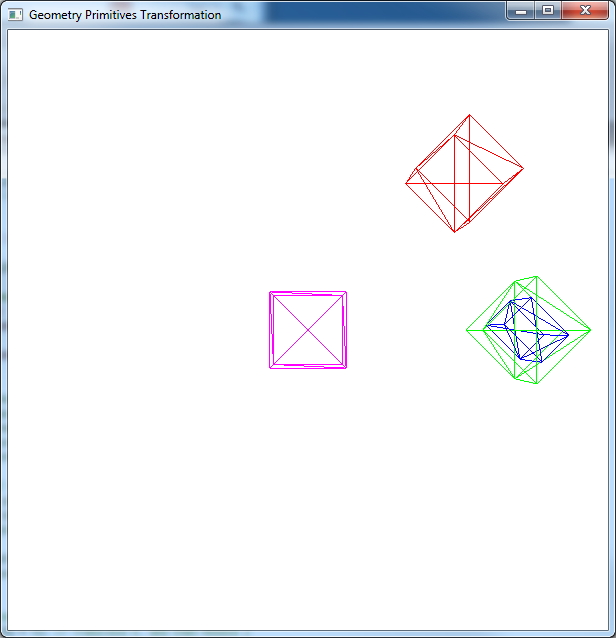
OpenGL/GLM Transformation (Column-Major Order)
glm::mat4 A(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 2.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 4.0f, 0.0f, // column3
1.0f, 2.0f, 3.0f, 1.0f); // column4
// A =
// 1 0 0 1
// 0 2 0 2
// 0 0 4 3
// 0 0 0 1
glm::mat4 B(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 1.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 1.0f, 0.0f, // column3
2.0f, 2.0f, 2.0f, 1.0f); // column4
// B =
// 1 0 0 2
// 0 1 0 2
// 0 0 1 2
// 0 0 0 1
glm::mat4 C = A*B;
// C = A*B =
// 1 0 0 3
// 0 2 0 6
// 0 0 4 11
// 0 0 0 1
glm::mat4 D = B*A;
// D = B*A =
// 1 0 0 3
// 0 2 0 4
// 0 0 4 5
// 0 0 0 1
glm::mat4 E = glm::inverse(A); // inverse
// E = inverse(A) =
// 1 0 0 -1
// 0 0.5 0 -1
// 0 0 0.25 -0.75
// 0 0 0 1
glm::mat4 I = A * E; // I = A * A-1
// I = A*E =
// 1 0 0 0
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1
// p’ = M * p (OpenGL/GLM uses Column-Major Order)
glm::vec4 p = glm::vec4(1.0f, 0.0f, 0.0f, 1.0f);
// p = (1, 0, 0)
glm::vec4 q = A * p;
// q = A * p = (2, 2, 3)
glm::vec4 r = B * p;
// r = B * p = (3, 2, 2)
glm::vec4 s = C * p;
// s = A * B * p = (4, 6, 11)
glm::vec4 t = D * p;
// t = B * A * p = (4, 4, 5)
glm::mat4 Tx,Ty,Tz;
Tx = glm::translate(glm::mat4(1.0f), glm::vec3(2.0f, 0.0f, 0.0f)); // RHS x+ right
Ty = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 2.0f, 0.0f)); // RHS y+ up
Tz = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 0.0f, 2.0f)); // RHS z+ front
// Tx =
// 1 0 0 2
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1
glm::mat4 Rx,Ry,Rz,Ra;
Rx = glm::rotate(glm::mat4(1.0f), 30.0f, glm::vec3(1.0f, 0.0f, 0.0f)); // RHS x+ (Y->Z rotation) OpenGL uses DEGREE angle
Ry = glm::rotate(glm::mat4(1.0f), 60.0f, glm::vec3(0.0f, 1.0f, 0.0f)); // RHS y+ (Z->X rotation)
Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // RHS z+ (X->Y rotation)
Ra = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(1.0f, 1.0f, 1.0f)); // RHS (arbitrary axis)
// Rx =
// 1 0 0 0
// 0 0.999958 -0.0091384 0
// 0 0.0091384 0.999958 0
// 0 0 0 1
// Ry =
// 0.999833 0 0.018276 0
// 0 1 0 0
// -0.018276 0 0.999833 0
// 0 0 0 1
// Rz =
// 0.999906 -0.0137074 0 0
// 0.0137074 0.999906 0 0
// 0 0 1 0
// 0 0 0 1
// Ra =
// 0.999937 -0.00788263 0.00794526 0
// 0.00794526 0.999937 -0.00788263 0
// -0.00788263 0.00794526 0.999937 0
// 0 0 0 1
glm::mat4 Sx,Sy,Sz;
Sx = glm::scale(glm::mat4(1.0f), glm::vec3(2, 1, 1)); // RHS
Sy = glm::scale(glm::mat4(1.0f), glm::vec3(1, 2, 1)); // RHS
Sz = glm::scale(glm::mat4(1.0f), glm::vec3(1, 1, 2)); // RHS
// Sy =
// 1 0 0 0
// 0 2 0 0
// 0 0 1 0
// 0 0 0 1
// p’ = M3 * M2 * M1 * p (OpenGL uses Column-Major Order)
glm::mat4 TR = Tx * Rz; // Rotate Z, and then Translate X
glm::mat4 RT = Rz * Tx; // Translate X, and then Rotate Z
glm::mat4 TRS = Tx * Rz * Sy; // Scale Y, and then Rotate Z, and then Translate X
glm::mat4 SRT = Sy * Rz * Tx; // Translate X, and then Rotate Z, and then Scale Y
// Tx*Rz =
// 0.707107 -0.707107 0 2
// 0.707107 0.707107 0 0
// 0 0 1 0
// 0 0 0 1
// Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 0.707107 0.707107 0 1.41421
// 0 0 1 0
// 0 0 0 1
// Tx*Rz*Sy =
// 0.707107 -1.41421 0 2
// 0.707107 1.41421 0 0
// 0 0 1 0
// 0 0 0 1
// Sy*Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 1.41421 1.41421 0 2.82843
// 0 0 1 0
// 0 0 0 1