https://en.wikipedia.org/wiki/Gimbal_lock
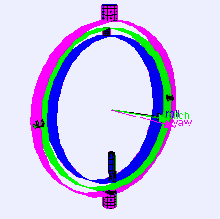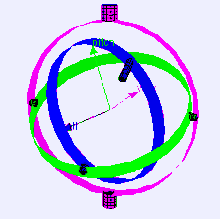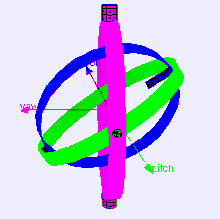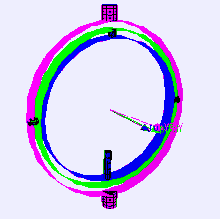
R = Rz * Rx * Ry vs. YawPitchRoll
cos60=0.500000 sin60=0.866025
cos30=0.866025 sin30=0.500000
cos45=0.707107 sin45=0.707107
// glm::rotate(glm::mat4(1.0f), 30.0f, glm::vec3(1.0f, 0.0f, 0.0f));
Rx=
1.000000 0.000000 0.000000 0.000000
0.000000 0.866025 -0.500000 0.000000
0.000000 0.500000 0.866025 0.000000
0.000000 0.000000 0.000000 1.000000
// glm::rotate(glm::mat4(1.0f), 60.0f, glm::vec3(0.0f, 1.0f, 0.0f));
Ry=
0.500000 0.000000 0.866025 0.000000
0.000000 1.000000 0.000000 0.000000
-0.866025 0.000000 0.500000 0.000000
0.000000 0.000000 0.000000 1.000000
// glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f));
Rz=
0.707107 -0.707107 0.000000 0.000000
0.707107 0.707107 0.000000 0.000000
0.000000 0.000000 1.000000 0.000000
0.000000 0.000000 0.000000 1.000000
// R = Rz * Rx * Ry (1. Ry 2. Rx 3. Rz) == XNA CreateRotationY(60) * CreateRotationX(30) * CreateRotationZ(45)
R =
0.047367 -0.612372 0.789149 0.000000
0.659740 0.612372 0.435596 0.000000
-0.750000 0.500000 0.433013 0.000000
0.000000 0.000000 0.000000 1.000000
// glm::eulerAngleYXZ(60, 30, 45) == XNA CreateFromYawPitchRoll(60, 30, 45)
Euler=
0.659740 -0.047367 0.750000 0.000000
0.612372 0.612372 -0.500000 0.000000
-0.435596 0.789149 0.433013 0.000000
0.000000 0.000000 0.000000 1.000000
// glm::yawPitchRoll(60, 30, 45) == XNA CreateFromYawPitchRoll(60, 30, 45)
YPR=
0.659740 -0.047367 0.750000 0.000000
0.612372 0.612372 -0.500000 0.000000
-0.435596 0.789149 0.433013 0.000000
0.000000 0.000000 0.000000 1.000000
glm::mat4 Tx = glm::translate(glm::mat4(1.0f), glm::vec3(3.0f, 0.0f, 0.0f));
glm::mat4 Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f));
glm::mat4 S = glm::scale(glm::mat4(1.0f), glm::vec3(0.5f, 0.7f, 1.0f));
glm::mat4 TRS = Tx * Rz * S; // Scale XY, and then Rotate Z, and then Translate X
위의 코드는 아래의 코드와 동일한 행렬의 곱 연산을 수행한다.
glm::mat4 T = glm::translate(glm::mat4(1.0f), glm::vec3(3.0f, 0.0f, 0.0f)); // T
glm::mat4 TR = glm::rotate(T, 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // T * R
glm::mat4 TRS = glm::scale(TR, glm::vec3(0.5f, 0.7f, 1.0f)); // T * R * S
Lab7-GeometryPositionColorSimpleCar (using Transformation matrix)
lab7-GeometryPositionColorSimpleCar
SimpleCar::SimpleCar()
{
angle = 0.0f; // 0~360
direction = 1.0f; // +/-1
position = glm::vec3(-3.0f, 0.0f, 0.0f);
init();
}
void SimpleCar::init()
{
body = Parallelepiped(glm::vec3(-1.0f, 0.0f, -1.0f), glm::vec3(2.0f, 0.0f, 0.0f), glm::vec3(0.0f, 0.0f, 2.0f), glm::vec3(0.0f, 1.0f, 0.0f));
body.setColor(glm::vec3(0.0f, 1.0f, 0.0f));
wheel[0] = Torus(glm::vec3(0.0f, 0.0f, .0f), 0.3f, 0.1f, 32, 16);
wheel[0].setColor(glm::vec3(1.0f, 0.0f, 0.0f));
wheel[1] = Torus(glm::vec3(0.0f, 0.0f, .0f), 0.3f, 0.1f, 32, 16);
wheel[1].setColor(glm::vec3(0.0f, 0.0f, 1.0f));
bodyTransform = glm::translate(glm::mat4(1.0f), position); // RHS x+ right
wheelTransform[0] = glm::translate(glm::mat4(1.0f), glm::vec3(-0.5f, 0.0f, -0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[1] = glm::translate(glm::mat4(1.0f), glm::vec3(-0.5f, 0.0f, 0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[2] = glm::translate(glm::mat4(1.0f), glm::vec3(0.5f, 0.0f, -0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[3] = glm::translate(glm::mat4(1.0f), glm::vec3(0.5f, 0.0f, 0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
}
void SimpleCar::draw(Program* p, glm::mat4& projection, glm::mat4& view, glm::mat4& model)
{
p->useProgram();
p->setUniform(“gProjection”, projection);
p->setUniform(“gView”, view);
glm::mat4 carMatrix = model * bodyTransform;
p->setUniform(“gModel”, carMatrix);
body.draw();
glm::mat4 wheelMatrix = model * bodyTransform * wheelTransform[0];
p->setUniform(“gModel”, wheelMatrix);
wheel[0].draw();
wheelMatrix = model * bodyTransform * wheelTransform[1];
p->setUniform(“gModel”, wheelMatrix);
wheel[0].draw();
wheelMatrix = model * bodyTransform * wheelTransform[2];
p->setUniform(“gModel”, wheelMatrix);
wheel[1].draw();
wheelMatrix = model * bodyTransform * wheelTransform[3];
p->setUniform(“gModel”, wheelMatrix);
wheel[1].draw();
}
bool SimpleCar::update(float deltaTime)
{
angle = angle – 180.0f * (float) (deltaTime) * 0.001f * direction;
position[0] = position[0] + (float) (deltaTime) * 0.001f * direction;
//std::cout << “position[0]=” << position[0] << std::endl;
if (position[0] * direction > 3)
direction = -direction;
bodyTransform = glm::translate(glm::mat4(1.0f), position); // RHS x+ right
wheelTransform[0] = glm::translate(glm::mat4(1.0f), glm::vec3(-0.5f, 0.0f, -0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[1] = glm::translate(glm::mat4(1.0f), glm::vec3(-0.5f, 0.0f, 0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[2] = glm::translate(glm::mat4(1.0f), glm::vec3( 0.5f, 0.0f, -0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
wheelTransform[3] = glm::translate(glm::mat4(1.0f), glm::vec3( 0.5f, 0.0f, 0.5f)) * glm::rotate(glm::mat4(1.0f), angle, glm::vec3(0.0f, 0.0f, 1.0f));
return true;
}
// MVP matrix
Projection = glm::perspective(g_fovy, g_aspect, g_zNear, g_zFar);
View = glm::lookAt(g_eye, g_at, g_up);
spMain.useProgram();
spMain.setUniform(“gProjection”, Projection);
spMain.setUniform(“gView”, View);
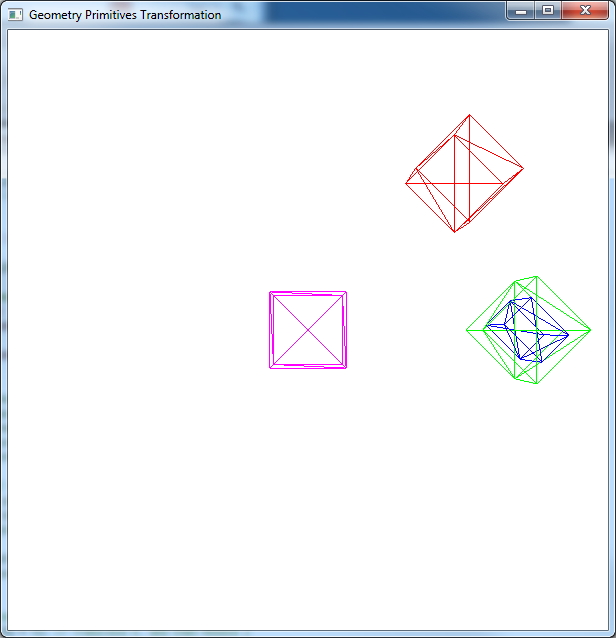
// p’ = M3 * M2 * M1 * p (OpenGL uses Column-Major Order)
glm::mat4 Tx = glm::translate(glm::mat4(1.0f), glm::vec3(3.0f, 0.0f, 0.0f)); // RHS x+ right
glm::mat4 Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // RHS z+ (X->Y rotation)
glm::mat4 S = glm::scale(glm::mat4(1.0f), glm::vec3(0.5f, 0.7f, 1.0f)); // RHS
World = glm::mat4(1.0f);
spMain.setUniform(“gModel”, World);
cube1->draw();
// p’= R T p (red) => translate, and then rotate
glm::mat4 RT = Rz * Tx; // Translate X, and then Rotate Z
World = RT;
spMain.setUniform(“gModel”, World);
cube2->draw();
// p’= T R p (green) => rotate, and then translate
glm::mat4 TR = Tx * Rz; // Rotate Z, and then Translate X
World = TR;
spMain.setUniform(“gModel”, World);
cube3->draw();
// p’= T R S p (blue) => scale, and then rotate, and then translate
glm::mat4 TRS = Tx * Rz * S; // Scale XY, and then Rotate Z, and then Translate X
World = TRS;
spMain.setUniform(“gModel”, World);
cube4->draw();
http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/
Until then, we only considered 3D vertices as a (x,y,z) triplet. Let’s introduce w. We will now have (x,y,z,w) vectors.
This will be more clear soon, but for now, just remember this :
(In fact, remember this forever.)
What difference does this make ? Well, for a rotation, it doesn’t change anything. When you rotate a point or a direction, you get the same result. However, for a translation (when you move the point in a certain direction), things are different. What could mean “translate a direction” ? Not much.Homogeneous coordinates allow us to use a single mathematical formula to deal with these two cases.
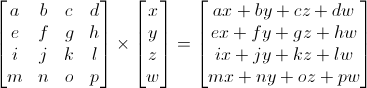
In 3D graphics we will mostly use 4×4 matrices. They will allow us to transform our (x,y,z,w) vertices. This is done by multiplying the vertex with the matrix :
Matrix x Vertex (in this order !!) = TransformedVertex
In C++, with GLM:
glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.
In GLSL :
mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM
These are the most simple tranformation matrices to understand. A translation matrix look like this :
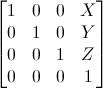
where X,Y,Z are the values that you want to add to your position.
So if we want to translate the vector (10,10,10,1) of 10 units in the X direction, we get :
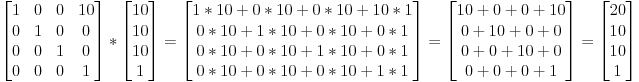
Scaling matrices are quite easy too :
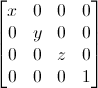
So if you want to scale a vector (position or direction, it doesn’t matter) by 2.0 in all directions :
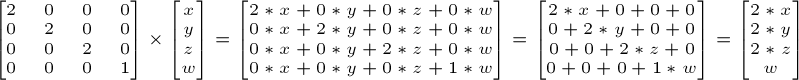
These are quite complicated.
So now we know how to rotate, translate, and scale our vectors. It would be great to combine these transformations. This is done by multiplying the matrices together, for instance :
TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;
This model, just as our beloved red triangle, is defined by a set of vertices. The X,Y,Z coordinates of these vertices are defined relative to the object’s center : that is, if a vertex is at (0,0,0), it is at the center of the object.
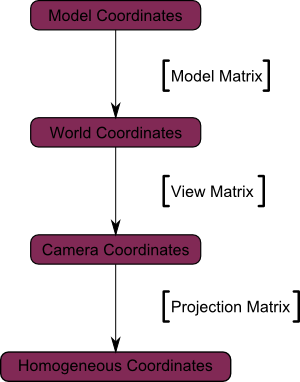
We can sum this up with the following diagram :
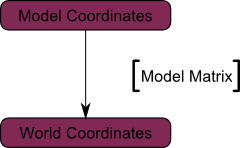
We went from World Space (all vertices defined relatively to the center of the world, as we made so in the previous section) to Camera Space (all vertices defined relatively to the camera).
Here’s the compulsory diagram :
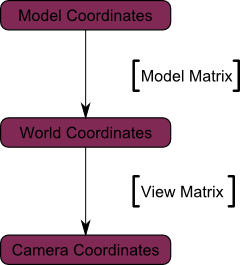
We’re now in Camera Space. This means that after all theses transformations, a vertex that happens to have x==0 and y==0 should be rendered at the center of the screen.
And the final diagram :
glm::mat4 A(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 2.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 4.0f, 0.0f, // column3
1.0f, 2.0f, 3.0f, 1.0f); // column4
// A =
// 1 0 0 1
// 0 2 0 2
// 0 0 4 3
// 0 0 0 1
glm::mat4 B(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 1.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 1.0f, 0.0f, // column3
2.0f, 2.0f, 2.0f, 1.0f); // column4
// B =
// 1 0 0 2
// 0 1 0 2
// 0 0 1 2
// 0 0 0 1
glm::mat4 C = A*B;
// C = A*B =
// 1 0 0 3
// 0 2 0 6
// 0 0 4 11
// 0 0 0 1
glm::mat4 D = B*A;
// D = B*A =
// 1 0 0 3
// 0 2 0 4
// 0 0 4 5
// 0 0 0 1
glm::mat4 E = glm::inverse(A); // inverse
// E = inverse(A) =
// 1 0 0 -1
// 0 0.5 0 -1
// 0 0 0.25 -0.75
// 0 0 0 1
glm::mat4 I = A * E; // I = A * A-1
// I = A*E =
// 1 0 0 0
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1
// p’ = M * p (OpenGL/GLM uses Column-Major Order)
glm::vec4 p = glm::vec4(1.0f, 0.0f, 0.0f, 1.0f);
// p = (1, 0, 0)
glm::vec4 q = A * p;
// q = A * p = (2, 2, 3)
glm::vec4 r = B * p;
// r = B * p = (3, 2, 2)
glm::vec4 s = C * p;
// s = A * B * p = (4, 6, 11)
glm::vec4 t = D * p;
// t = B * A * p = (4, 4, 5)
glm::mat4 Tx,Ty,Tz;
Tx = glm::translate(glm::mat4(1.0f), glm::vec3(2.0f, 0.0f, 0.0f)); // RHS x+ right
Ty = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 2.0f, 0.0f)); // RHS y+ up
Tz = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 0.0f, 2.0f)); // RHS z+ front
// Tx =
// 1 0 0 2
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1
// Ty =
// 1 0 0 0
// 0 1 0 2
// 0 0 1 0
// 0 0 0 1
// Tz =
// 1 0 0 0
// 0 1 0 0
// 0 0 1 2
// 0 0 0 1
glm::mat4 Rx,Ry,Rz,Ra;
Rx = glm::rotate(glm::mat4(1.0f), 30.0f, glm::vec3(1.0f, 0.0f, 0.0f)); // RHS x+ (Y->Z rotation) OpenGL uses DEGREE angle
Ry = glm::rotate(glm::mat4(1.0f), 60.0f, glm::vec3(0.0f, 1.0f, 0.0f)); // RHS y+ (Z->X rotation)
Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // RHS z+ (X->Y rotation)
Ra = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(1.0f, 1.0f, 1.0f)); // RHS (arbitrary axis)
// Rx =
// 1 0 0 0
// 0 0.999958 -0.0091384 0
// 0 0.0091384 0.999958 0
// 0 0 0 1
// Ry =
// 0.999833 0 0.018276 0
// 0 1 0 0
// -0.018276 0 0.999833 0
// 0 0 0 1
// Rz =
// 0.999906 -0.0137074 0 0
// 0.0137074 0.999906 0 0
// 0 0 1 0
// 0 0 0 1
// Ra =
// 0.999937 -0.00788263 0.00794526 0
// 0.00794526 0.999937 -0.00788263 0
// -0.00788263 0.00794526 0.999937 0
// 0 0 0 1
glm::mat4 Sx,Sy,Sz;
Sx = glm::scale(glm::mat4(1.0f), glm::vec3(2, 1, 1)); // RHS
Sy = glm::scale(glm::mat4(1.0f), glm::vec3(1, 2, 1)); // RHS
Sz = glm::scale(glm::mat4(1.0f), glm::vec3(1, 1, 2)); // RHS
// Sy =
// 1 0 0 0
// 0 2 0 0
// 0 0 1 0
// 0 0 0 1
// p’ = M3 * M2 * M1 * p (OpenGL uses Column-Major Order)
glm::mat4 TR = Tx * Rz; // Rotate Z, and then Translate X
glm::mat4 RT = Rz * Tx; // Translate X, and then Rotate Z
glm::mat4 TRS = Tx * Rz * Sy; // Scale Y, and then Rotate Z, and then Translate X
glm::mat4 SRT = Sy * Rz * Tx; // Translate X, and then Rotate Z, and then Scale Y
// Tx*Rz =
// 0.707107 -0.707107 0 2
// 0.707107 0.707107 0 0
// 0 0 1 0
// 0 0 0 1
// Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 0.707107 0.707107 0 1.41421
// 0 0 1 0
// 0 0 0 1
// Tx*Rz*Sy =
// 0.707107 -1.41421 0 2
// 0.707107 1.41421 0 0
// 0 0 1 0
// 0 0 0 1
// Sy*Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 1.41421 1.41421 0 2.82843
// 0 0 1 0
// 0 0 0 1