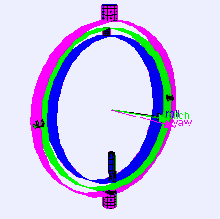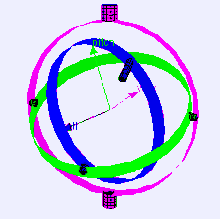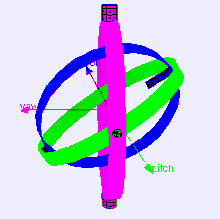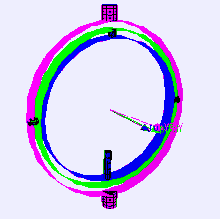
https://en.wikipedia.org/wiki/Gimbal_lock

How to Rotate in Unity (complete beginner’s guide)

// Create a Ra matrix Euler(30, 60, 45)
Matrix4x4 ra = Matrix4x4.Rotate(Quaternion.Euler(30, 60, 45));
// Create a Rb matrix rz -> rx -> ry
Matrix4x4 rz = Matrix4x4.Rotate(Quaternion.Euler(0, 0, 45));
Matrix4x4 rx = Matrix4x4.Rotate(Quaternion.Euler(30, 0, 0));
Matrix4x4 ry = Matrix4x4.Rotate(Quaternion.Euler(0, 60, 0));
Matrix4x4 rb = ry * rx * rz; // Z → X → Y

// ra == rb

// Create a Rc matrix ry -> rx -> rz
Matrix4x4 rc = rz * rx * ry; // Y → X → Z

// rb != rc

// translation, rotation, scale
Vector3 translation = new Vector3(1.5, 0, 0);
Quaternion rotation = Quaternion.Euler(0, 0, 45);
Vector3 scale = new Vector3(0.2, 0.2, 0.2);
// Create a composing transformation Scale -> Rotation -> Translation
Matrix4x4 m1 = Matrix4x4.TRS(translation, rotation, scale);
// Create a composing transformation Scale -> Rotate -> Translate
Matrix4x4 m2 = Matrix4x4.Translate(translation) *
Matrix4x4.Rotate(rotation) * Matrix4x4.Scale(scale); // Scale -> Rotation -> Translation
if (m1 == m2) Debug.Log(“m1 == m2”);

Matrix4x4 m3 = Matrix4x4.Scale(scale) *
Matrix4x4.Rotate(rotation) * Matrix4x4.Translate(translation); // Translation -> Rotation -> Scale
if (m1 != m3) Debug.Log(“m1 != m3”);

Rotate a point about an arbitrary axis (3 dimensions)
Written by Paul Bourke

https://paulbourke.net/geometry/rotate/

/*
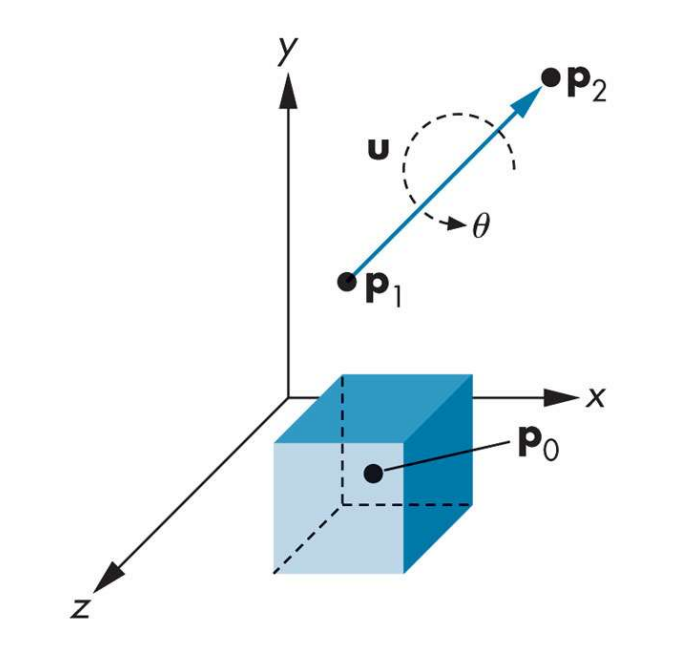
Rotate a point p by angle around an arbitrary line segment p1-p2
Return the rotated point.
Positive angles are anticlockwise looking down the axis
towards the origin. Assume right hand coordinate system.
*/
public static Vector3 ArbitraryRotate(Vector3 p, float angle, Vector3 p1, Vector3 p2)
{
Vector3 u, q1, q2, q3, q4, q5, q6, q7;
float d;

// (1) translate space so that the rotation axis passes through the origin
q1 = p – p1;

// (2) rotate space about the x axis so that the rotation axis lies in the xz plane
u = p2 – p1; // rotation-axis vector
u = Vector3.Normalize(u);
d = Mathf.Sqrt(u.y*u.y + u.z*u.z);
if (d != 0) {
q2.x = q1.x;
q2.y = q1.y * u.z / d – q1.z * u.y / d;
q2.z = q1.y * u.y / d + q1.z * u.z / d;
} else {
q2 = q1;
}

// (3) rotate space about the y axis so that the rotation axis lies along the z axis
q3.x = q2.x * d – q2.z * u.x;
q3.y = q2.y;
q3.z = q2.x * u.x + q2.z * d;

// (4) perform the desired rotation by theta about the z axis
float theta = Mathf.Deg2Rad * angle;
q4.x = q3.x * Mathf.Cos(theta) – q3.y * Mathf.Sin(theta);
q4.y = q3.x * Mathf.Sin(theta) + q3.y * Mathf.Cos(theta);
q4.z = q3.z;

// (5) apply the inverse of step (3)
q5.x = q4.x * d + q4.z * u.x;
q5.y = q4.y;
q5.z = -q4.x * u.x + q4.z * d;

// (6) apply the inverse of step (2)
if (d != 0) {
q6.x = q5.x;
q6.y = q5.y * u.z / d + q5.z * u.y / d;
q6.z = -q5.y * u.y / d + q5.z * u.z / d;
} else {
q6 = q5;
}

// (7) apply the inverse of step (1)
q7 = q6 + p1;
return q7;
}

/*
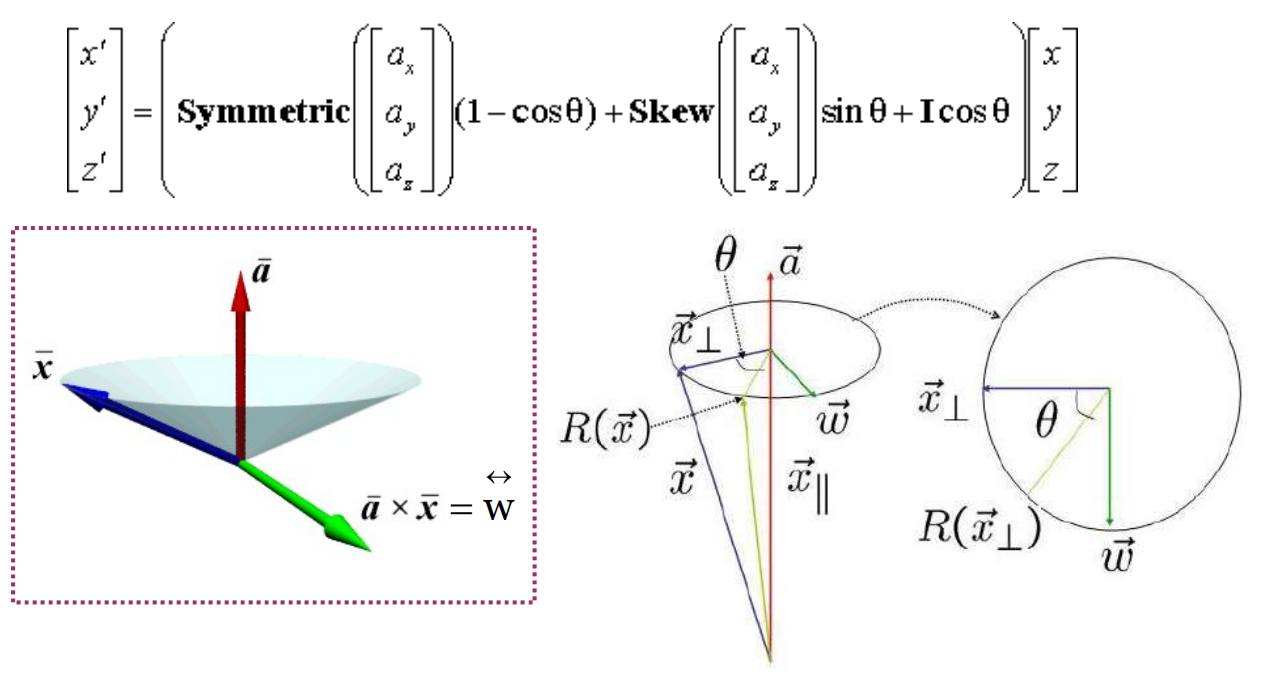
Rotate a point p by angle around an arbitrary axis
Return the rotated point.
Positive angles are anticlockwise looking down the axis
towards the origin. Assume right hand coordinate system.
*/
public static Vector3 ArbitraryRotate(Vector3 p, float angle, Vector3 axis)
{
Vector3 q = Vector3.zero;
float costheta, sintheta;
float theta = Mathf.Deg2Rad * angle;

axis = Vector3.Normalize(axis);
costheta = Mathf.Cos(theta);
sintheta = Mathf.Sin(theta);

q.x += (costheta + (1 – costheta) * axis.x * axis.x) * p.x;
q.x += ((1 – costheta) * axis.x * axis.y – axis.z * sintheta) * p.y;
q.x += ((1 – costheta) * axis.x * axis.z + axis.y * sintheta) * p.z;

q.y += ((1 – costheta) * axis.x * axis.y + axis.z * sintheta) * p.x;
q.y += (costheta + (1 – costheta) * axis.y * axis.y) * p.y;
q.y += ((1 – costheta) * axis.y * axis.z – axis.x * sintheta) * p.z;

q.z += ((1 – costheta) * axis.x * axis.z – axis.y * sintheta) * p.x;
q.z += ((1 – costheta) * axis.y * axis.z + axis.x * sintheta) * p.y;
q.z += (costheta + (1 – costheta) * axis.z * axis.z) * p.z;

return q;
}

Vector3 Position = new Vector3(0.0f, 0.0f, 0.0f);
Matrix4x4 Model = Matrix4x4.Translate(new Vector3(1.0f, 2.0f, 3.0f));
// Debug.Log(Model);
// (1.0, 0.0, 0.0, 1.0)
// (0.0, 1.0, 0.0, 2.0)
// (0.0, 0.0, 1.0, 3.0)
// (0.0, 0.0, 0.0, 1.0)

Vector3 Transformed = Model * Position; // P’ (1, 2, 3) = Model * P (0, 0, 0) (Unity Matrix uses Column-Major Order) 

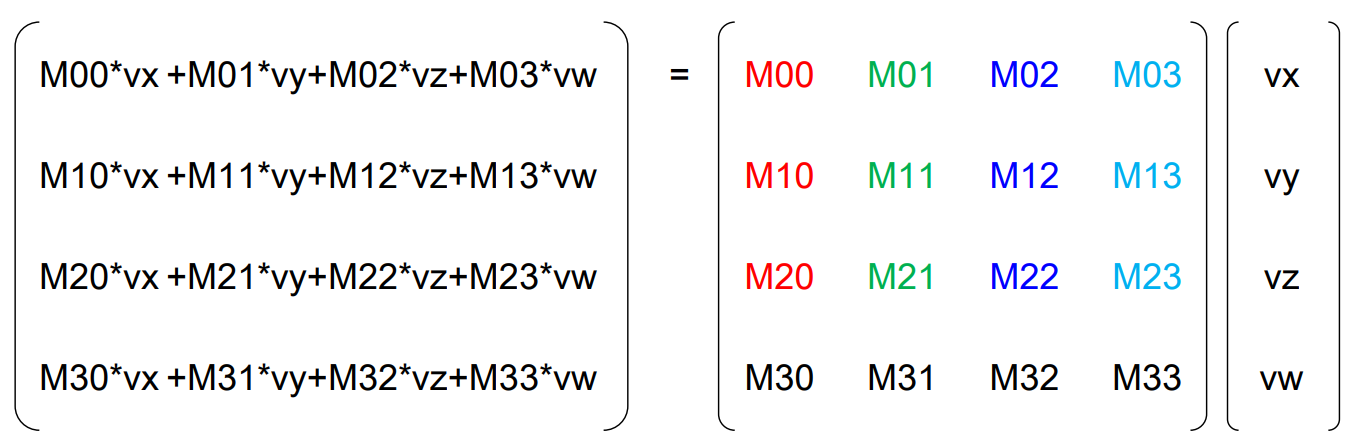
http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/

Homogeneous coordinates

Until then, we only considered 3D vertices as a (x,y,z) triplet. Let’s introduce w. We will now have (x,y,z,w) vectors.

This will be more clear soon, but for now, just remember this :

• If w == 1, then the vector (x,y,z,1) is a position in space.
• If w == 0, then the vector (x,y,z,0) is a direction.

(In fact, remember this forever.)
What difference does this make ? Well, for a rotation, it doesn’t change anything. When you rotate a point or a direction, you get the same result. However, for a translation (when you move the point in a certain direction), things are different. What could mean “translate a direction” ? Not much.Homogeneous coordinates allow us to use a single mathematical formula to deal with these two cases.

Transformation matrices

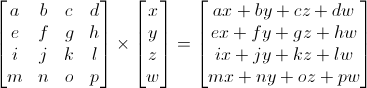
In 3D graphics we will mostly use 4×4 matrices. They will allow us to transform our (x,y,z,w) vertices. This is done by multiplying the vertex with the matrix :

Matrix x Vertex (in this order !!) = TransformedVertex

In C++, with GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.

In GLSL :

mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

Translation matrices

These are the most simple tranformation matrices to understand. A translation matrix look like this :

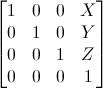
where X,Y,Z are the values that you want to add to your position.

So if we want to translate the vector (10,10,10,1) of 10 units in the X direction, we get :

Scaling matrices

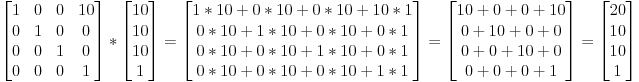
Scaling matrices are quite easy too :

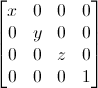
So if you want to scale a vector (position or direction, it doesn’t matter) by 2.0 in all directions :

Rotation matrices

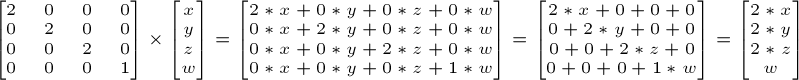
These are quite complicated.

Cumulating transformations

So now we know how to rotate, translate, and scale our vectors. It would be great to combine these transformations. This is done by multiplying the matrices together, for instance :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;