Matrix4x4.LookAt(Vector3 from, Vector4 to, Vector3 up) creates a “look at” matrix.
which is equal to Matrix4x4.TRS(from, Quaternion.LookRotation((to-from).normalized, up.normalized), Vector3.one)
Note that: glm::lookat != Matrix4x4.LookAt

Just another Kyoung Shin Park's Lectures Sites site
Matrix4x4.LookAt(Vector3 from, Vector4 to, Vector3 up) creates a “look at” matrix.
which is equal to Matrix4x4.TRS(from, Quaternion.LookRotation((to-from).normalized, up.normalized), Vector3.one)
Note that: glm::lookat != Matrix4x4.LookAt
template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAt(tvec3<T, P> const & eye, tvec3<T, P> const & center, tvec3<T, P> const & up)
{
# if GLM_COORDINATE_SYSTEM == GLM_LEFT_HANDED
return lookAtLH(eye, center, up);
# else
return lookAtRH(eye, center, up);
# endif
}
template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAtRH
(
tvec3<T, P> const & eye,
tvec3<T, P> const & center,
tvec3<T, P> const & up
)
{
tvec3<T, P> const f(normalize(center – eye));
tvec3<T, P> const s(normalize(cross(f, up)));
tvec3<T, P> const u(cross(s, f));
tmat4x4<T, P> Result(1);
Result[0][0] = s.x;
Result[1][0] = s.y;
Result[2][0] = s.z;
Result[0][1] = u.x;
Result[1][1] = u.y;
Result[2][1] = u.z;
Result[0][2] =-f.x;
Result[1][2] =-f.y;
Result[2][2] =-f.z;
Result[3][0] =-dot(s, eye);
Result[3][1] =-dot(u, eye);
Result[3][2] = dot(f, eye);
return Result;
}
template <typename T, precision P>
GLM_FUNC_QUALIFIER tmat4x4<T, P> lookAtLH
(
tvec3<T, P> const & eye,
tvec3<T, P> const & center,
tvec3<T, P> const & up
)
{
tvec3<T, P> const f(normalize(center – eye));
tvec3<T, P> const s(normalize(cross(up, f)));
tvec3<T, P> const u(cross(f, s));
tmat4x4<T, P> Result(1);
Result[0][0] = s.x;
Result[1][0] = s.y;
Result[2][0] = s.z;
Result[0][1] = u.x;
Result[1][1] = u.y;
Result[2][1] = u.z;
Result[0][2] = f.x;
Result[1][2] = f.y;
Result[2][2] = f.z;
Result[3][0] = -dot(s, eye);
Result[3][1] = -dot(u, eye);
Result[3][2] = -dot(f, eye);
return Result;
}

Z-fighting, also called stitching, is a phenomenon in 3D rendering that occurs when two or more primitives have similar values in the z-buffer. This problem is usually caused by limited sub-pixel precision and floating point and fixed point round-off errors.
The more z-buffer precision one uses, the less likely it is that z-fighting will be encountered. But for coplanar polygons, the problem is inevitable unless corrective action is taken.
As the distance between near and far clip planes increases, and in particular the near plane is selected near the eye, the greater the likelihood exists that z-fighting between primitives will occur.
Z-fighting can be reduced through the use of a higher resolution depth buffer, by z-buffering in some scenarios, or by simply moving the polygons further apart.
Z-fighting that is caused by insufficient precision in the depth buffer can be resolved by simply reducing the visible distance in the world. This reduces the distance between the near and far planes and solves the precision issue.
Another technique that is utilized to reduce or completely eliminate Z-fighting is switching to a logarithmic Z-buffer, reversing Z. This technique is seen in the game Grand Theft Auto V. Due to the way they are encoded, floating-point numbers have much more precision when closer to 0. Here, reversing Z leads to more precision when storing the depth of very distant objects, hence greatly reducing Z-fighting.
https://en.wikipedia.org/wiki/Z-fighting
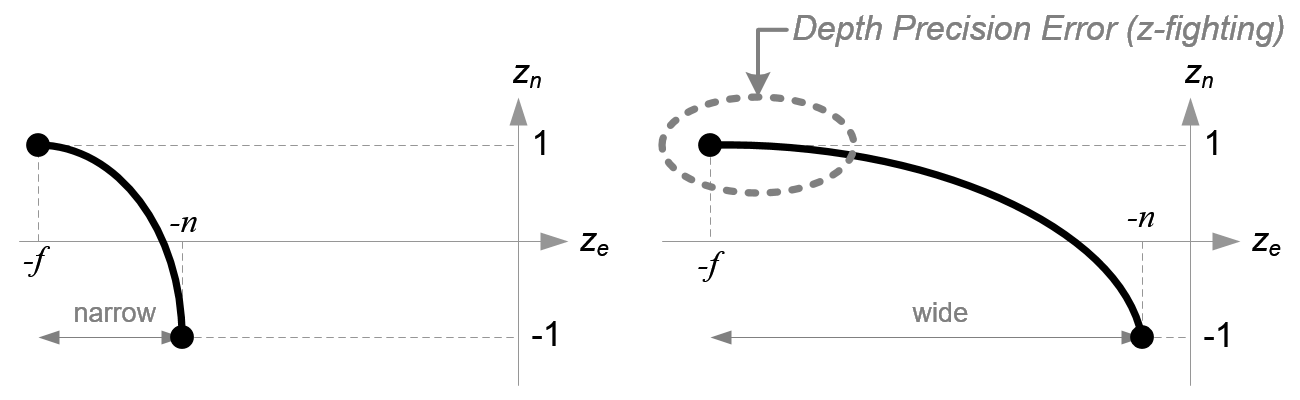
There is very high precision at the near plane, but very little precision at the far plane. If the range [-n, -f] is getting larger, it causes a depth precision problem (z-fighting); a small change of ze around the far plane does not affect on zn value. The distance between n and f should be short as possible to minimize the depth buffer precision problem.
http://www.songho.ca/opengl/gl_projectionmatrix.html


reversed-Z
Orthographic Projection
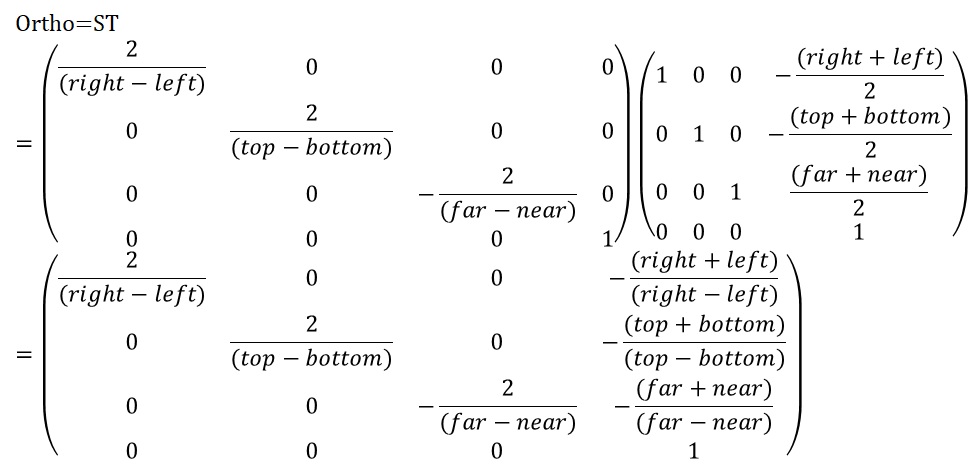
template <typename T>
GLM_FUNC_QUALIFIER tmat4x4<T, defaultp> ortho
(
T left,
T right,
T bottom,
T top,
T zNear,
T zFar
)
{
tmat4x4<T, defaultp> Result(1);
Result[0][0] = static_cast<T>(2) / (right - left);
Result[1][1] = static_cast<T>(2) / (top - bottom);
Result[2][2] = - static_cast<T>(2) / (zFar - zNear);
Result[3][0] = - (right + left) / (right - left);
Result[3][1] = - (top + bottom) / (top - bottom);
Result[3][2] = - (zFar + zNear) / (zFar - zNear);
return Result;
}
Perspective Projection
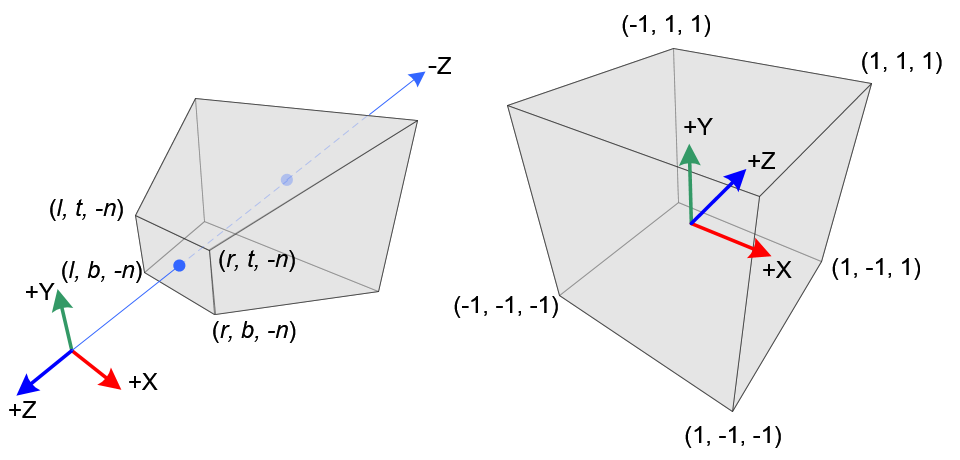

template <typename T>
GLM_FUNC_QUALIFIER tmat4x4<T, defaultp> frustum
(
T left,
T right,
T bottom,
T top,
T nearVal,
T farVal
)
{
tmat4x4<T, defaultp> Result(0);
Result[0][0] = (static_cast<T>(2) * nearVal) / (right - left);
Result[1][1] = (static_cast<T>(2) * nearVal) / (top - bottom);
Result[2][0] = (right + left) / (right - left);
Result[2][1] = (top + bottom) / (top - bottom);
Result[2][2] = -(farVal + nearVal) / (farVal - nearVal);
Result[2][3] = static_cast<T>(-1);
Result[3][2] = -(static_cast<T>(2) * farVal * nearVal) / (farVal - nearVal);
return Result;
}
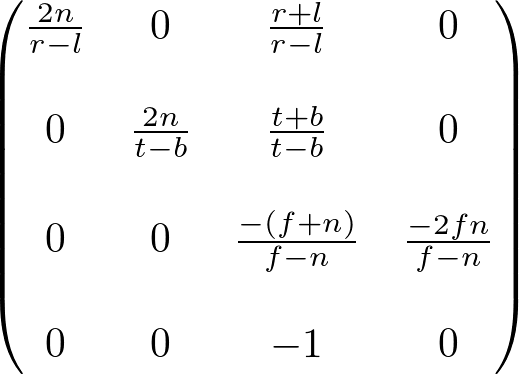
http://www.songho.ca/opengl/gl_projectionmatrix.html
mat4 projectionMatrix = glm::perspective (float fovy, float aspect, float near, float far) fovy radian
top = tan(fovy/2) * near
right = top * aspect
projectionMatrix = glm::frustum(-right, right, -top, top, near, far)
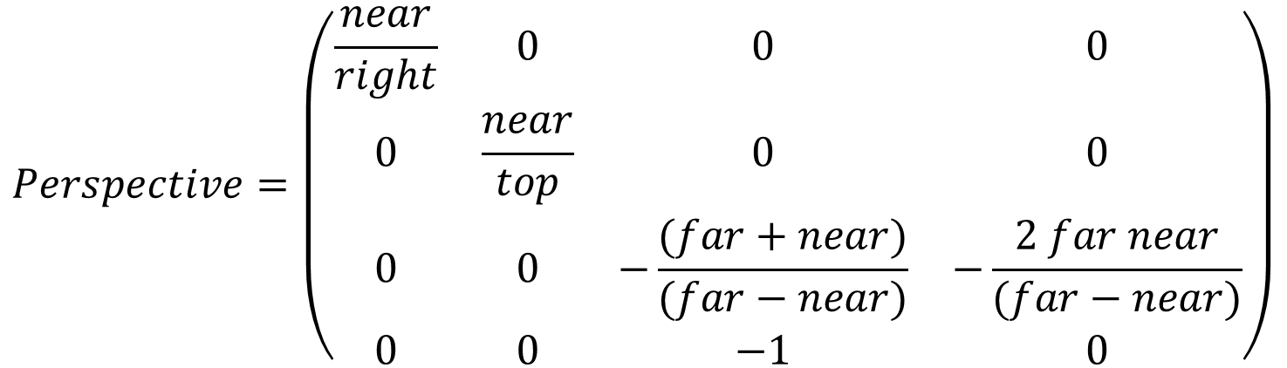
lecture11
lecture11-ch5
lecture10
lecture10-ch5
Images from https://en.wikipedia.org/wiki/Axonometric_projection