http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/

Homogeneous coordinates

Until then, we only considered 3D vertices as a (x,y,z) triplet. Let’s introduce w. We will now have (x,y,z,w) vectors.

This will be more clear soon, but for now, just remember this :

• If w == 1, then the vector (x,y,z,1) is a position in space.
• If w == 0, then the vector (x,y,z,0) is a direction.

(In fact, remember this forever.)
What difference does this make ? Well, for a rotation, it doesn’t change anything. When you rotate a point or a direction, you get the same result. However, for a translation (when you move the point in a certain direction), things are different. What could mean “translate a direction” ? Not much.Homogeneous coordinates allow us to use a single mathematical formula to deal with these two cases.

Transformation matrices

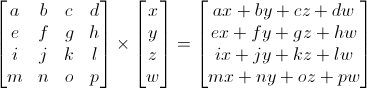
In 3D graphics we will mostly use 4×4 matrices. They will allow us to transform our (x,y,z,w) vertices. This is done by multiplying the vertex with the matrix :

Matrix x Vertex (in this order !!) = TransformedVertex

In C++, with GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.

In GLSL :

mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

Translation matrices

These are the most simple tranformation matrices to understand. A translation matrix look like this :

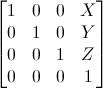
where X,Y,Z are the values that you want to add to your position.

So if we want to translate the vector (10,10,10,1) of 10 units in the X direction, we get :

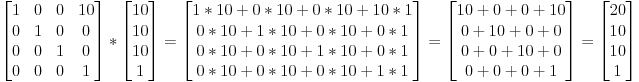
Scaling matrices

Scaling matrices are quite easy too :

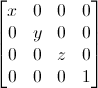
So if you want to scale a vector (position or direction, it doesn’t matter) by 2.0 in all directions :

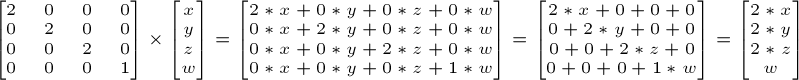
Rotation matrices

These are quite complicated.

Cumulating transformations

So now we know how to rotate, translate, and scale our vectors. It would be great to combine these transformations. This is done by multiplying the matrices together, for instance :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

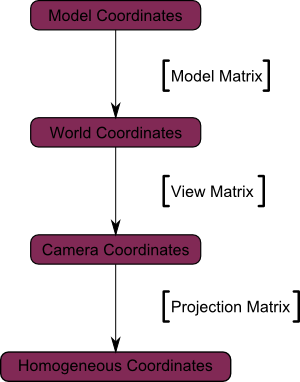
The Model, View and Projection matrices

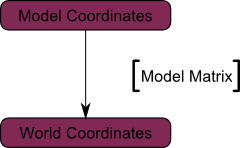
The Model matrix

This model, just as our beloved red triangle, is defined by a set of vertices. The X,Y,Z coordinates of these vertices are defined relative to the object’s center : that is, if a vertex is at (0,0,0), it is at the center of the object.

We can sum this up with the following diagram :

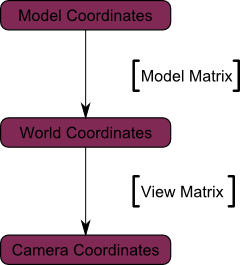
The View matrix

We went from World Space (all vertices defined relatively to the center of the world, as we made so in the previous section) to Camera Space (all vertices defined relatively to the camera).

Here’s the compulsory diagram :

The Projection matrix

We’re now in Camera Space. This means that after all theses transformations, a vertex that happens to have x==0 and y==0 should be rendered at the center of the screen.

And the final diagram :