Posted on

OPENGL/GLM TRANSFORMATION (COLUMN-MAJOR ORDER)

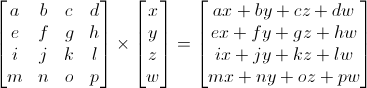
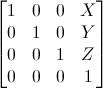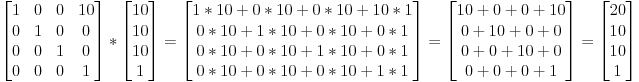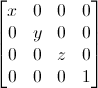glm::mat4 A(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 2.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 4.0f, 0.0f, // column3
1.0f, 2.0f, 3.0f, 1.0f); // column4
// A =
// 1 0 0 1
// 0 2 0 2
// 0 0 4 3
// 0 0 0 1

 

glm::mat4 B(1.0f, 0.0f, 0.0f, 0.0f, // column1
0.0f, 1.0f, 0.0f, 0.0f, // column2
0.0f, 0.0f, 1.0f, 0.0f, // column3
2.0f, 2.0f, 2.0f, 1.0f); // column4
// B =
// 1 0 0 2
// 0 1 0 2
// 0 0 1 2
// 0 0 0 1

 

glm::mat4 C = A*B;
// C = A*B =
// 1 0 0 3
// 0 2 0 6
// 0 0 4 11
// 0 0 0 1

 

glm::mat4 D = B*A;
// D = B*A =
// 1 0 0 3
// 0 2 0 4
// 0 0 4 5
// 0 0 0 1

 

glm::mat4 E = glm::inverse(A); // inverse
// E = inverse(A) =
// 1 0 0 -1
// 0 0.5 0 -1
// 0 0 0.25 -0.75
// 0 0 0 1

 

glm::mat4 I = A * E; // I = A * A-1
// I = A*E =
// 1 0 0 0
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1

 

// p’ = M * p (OpenGL/GLM uses Column-Major Order)
glm::vec4 p = glm::vec4(1.0f, 0.0f, 0.0f, 1.0f);
// p = (1, 0, 0)

glm::vec4 q = A * p;
// q = A * p = (2, 2, 3)

glm::vec4 r = B * p;
// r = B * p = (3, 2, 2)

glm::vec4 s = C * p;
// s = A * B * p = (4, 6, 11)

glm::vec4 t = D * p;
// t = B * A * p = (4, 4, 5)

 

glm::mat4 Tx,Ty,Tz;
Tx = glm::translate(glm::mat4(1.0f), glm::vec3(2.0f, 0.0f, 0.0f)); // RHS x+ right
Ty = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 2.0f, 0.0f)); // RHS y+ up
Tz = glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 0.0f, 2.0f)); // RHS z+ front
// Tx =
// 1 0 0 2
// 0 1 0 0
// 0 0 1 0
// 0 0 0 1

// Ty =
// 1 0 0 0
// 0 1 0 2
// 0 0 1 0
// 0 0 0 1

// Tz =
// 1 0 0 0
// 0 1 0 0
// 0 0 1 2
// 0 0 0 1

glm::mat4 Rx,Ry,Rz,Ra;
Rx = glm::rotate(glm::mat4(1.0f), 30.0f, glm::vec3(1.0f, 0.0f, 0.0f)); // RHS x+ (Y->Z rotation)
Ry = glm::rotate(glm::mat4(1.0f), 60.0f, glm::vec3(0.0f, 1.0f, 0.0f)); // RHS y+ (Z->X rotation)
Rz = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(0.0f, 0.0f, 1.0f)); // RHS z+ (X->Y rotation)
Ra = glm::rotate(glm::mat4(1.0f), 45.0f, glm::vec3(1.0f, 1.0f, 1.0f)); // RHS (arbitrary axis)
// Rx =
// 1 0 0 0
// 0 0.999958 -0.0091384 0
// 0 0.0091384 0.999958 0
// 0 0 0 1

 

// Ry =
// 0.999833 0 0.018276 0
// 0 1 0 0
// -0.018276 0 0.999833 0
// 0 0 0 1

 

// Rz =
// 0.999906 -0.0137074 0 0
// 0.0137074 0.999906 0 0
// 0 0 1 0
// 0 0 0 1

 

// Ra =
// 0.999937 -0.00788263 0.00794526 0
// 0.00794526 0.999937 -0.00788263 0
// -0.00788263 0.00794526 0.999937 0
// 0 0 0 1

 

glm::mat4 Sx,Sy,Sz;
Sx = glm::scale(glm::mat4(1.0f), glm::vec3(2, 1, 1)); // RHS
Sy = glm::scale(glm::mat4(1.0f), glm::vec3(1, 2, 1)); // RHS
Sz = glm::scale(glm::mat4(1.0f), glm::vec3(1, 1, 2)); // RHS
// Sy =
// 1 0 0 0
// 0 2 0 0
// 0 0 1 0
// 0 0 0 1

 

// p’ = M3 * M2 * M1 * p (OpenGL uses Column-Major Order)
glm::mat4 TR = Tx * Rz; // Rotate Z, and then Translate X
glm::mat4 RT = Rz * Tx; // Translate X, and then Rotate Z
glm::mat4 TRS = Tx * Rz * Sy; // Scale Y, and then Rotate Z, and then Translate X
glm::mat4 SRT = Sy * Rz * Tx; // Translate X, and then Rotate Z, and then Scale Y
// Tx*Rz =
// 0.707107 -0.707107 0 2
// 0.707107 0.707107 0 0
// 0 0 1 0
// 0 0 0 1

 

// Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 0.707107 0.707107 0 1.41421
// 0 0 1 0
// 0 0 0 1

 

// Tx*Rz*Sy =
// 0.707107 -1.41421 0 2
// 0.707107 1.41421 0 0
// 0 0 1 0
// 0 0 0 1

 

// Sy*Rz*Tx =
// 0.707107 -0.707107 0 1.41421
// 1.41421 1.41421 0 2.82843
// 0 0 1 0
// 0 0 0 1

Posted on

GLM MATRIX (COLUMN-MAJOR ORDER)

int foo()
{
glm::vec4 Position = glm::vec4(glm:: vec3(0.0f), 1.0f);
glm::mat4 Model = glm::translate(glm::mat4(1.0f), glm::vec3(1.0f, 2.0f, 3.0f));
// (1.0, 0.0, 0.0, 1.0)
// (0.0, 1.0, 0.0, 2.0)
// (0.0, 0.0, 1.0, 3.0)
// (0.0, 0.0, 0.0, 1.0)

printf(“%f %f %f %f\n”, Model[0][0], Model[1][0], Model[2][0], Model[3][0]);
printf(“%f %f %f %f\n”, Model[0][1], Model[1][1], Model[2][1], Model[3][1]);
printf(“%f %f %f %f\n”, Model[0][2], Model[1][2], Model[2][2], Model[3][2]);
printf(“%f %f %f %f\n”, Model[0][3], Model[1][3], Model[2][3], Model[3][3]);

glm::vec4 Transformed = Model * Position; // P’ (1, 2, 3) = Model * P (0, 0, 0) (OpenGL uses Column-Major Order) RHS
…
return 0;
}

Posted on

OPENGL TRANSFORMATION MATRIX TUTORIAL

http://www.opengl-tutorial.org/beginners-tutorials/tutorial-3-matrices/

Homogeneous coordinates

Until then, we only considered 3D vertices as a (x,y,z) triplet. Let’s introduce w. We will now have (x,y,z,w) vectors.

This will be more clear soon, but for now, just remember this :

  • If w == 1, then the vector (x,y,z,1) is a position in space.
  • If w == 0, then the vector (x,y,z,0) is a direction.

(In fact, remember this forever.)
What difference does this make ? Well, for a rotation, it doesn’t change anything. When you rotate a point or a direction, you get the same result. However, for a translation (when you move the point in a certain direction), things are different. What could mean “translate a direction” ? Not much.Homogeneous coordinates allow us to use a single mathematical formula to deal with these two cases.

Transformation matrices

In 3D graphics we will mostly use 4×4 matrices. They will allow us to transform our (x,y,z,w) vertices. This is done by multiplying the vertex with the matrix :

Matrix x Vertex (in this order !!) = TransformedVertex

In C++, with GLM:

glm::mat4 myMatrix;
glm::vec4 myVector;
// fill myMatrix and myVector somehow
glm::vec4 transformedVector = myMatrix * myVector; // Again, in this order ! this is important.

In GLSL :

mat4 myMatrix;
vec4 myVector;
// fill myMatrix and myVector somehow
vec4 transformedVector = myMatrix * myVector; // Yeah, it's pretty much the same than GLM

Translation matrices

These are the most simple tranformation matrices to understand. A translation matrix look like this :

where X,Y,Z are the values that you want to add to your position.

So if we want to translate the vector (10,10,10,1) of 10 units in the X direction, we get :

Scaling matrices

Scaling matrices are quite easy too :

So if you want to scale a vector (position or direction, it doesn’t matter) by 2.0 in all directions :

Rotation matrices

These are quite complicated.

Cumulating transformations

So now we know how to rotate, translate, and scale our vectors. It would be great to combine these transformations. This is done by multiplying the matrices together, for instance :

TransformedVector = TranslationMatrix * RotationMatrix * ScaleMatrix * OriginalVector;

 

 

Posted on

Affine Space

Affine Space (아핀공간) – 벡터공간에 점을 추가한 공간
http://mathworld.wolfram.com/AffineSpace.html

벡터와 벡터 간의 덧셈/뺄셈 -> 벡터 생성
스칼라와 벡터의 곱셈/나눗셈 -> 벡터 생성
벡터와 점의 덧셈/뺄셈 -> 점 생성
점과 점 간의 뺄셈 -> 벡터 생성
점과 점 간의 덧셈은 허용되지 않는다.
아핀공간에서 점의 덧셈은 각 점들 앞의 계수의 합이 1일 때에만 허용되고 이처럼 계수의 합이 1이 되는 경우를 Affine Sum(아핀합)이라 한다.

Homogeneous Coordinate (동차좌표) – 어떤 목적을 위해 한 차원의 좌표(n)을 추가한 좌표 (n+1)로 표현을 하는 것
http://mathworld.wolfram.com/HomogeneousCoordinates.html

4차원 동차 좌표 (x,y,z,w) => 3차원 좌표 (x/w , y/w , z/w)
만약 w == 1, (x,y,z,1)은 position이다.
만약 w == 0, (x,y,z,0)은 vector이다.