Computer Graphics 2021

Billboarding & AlphaBlendTextures

lab16-BillboardingTextureShadedQuad

 

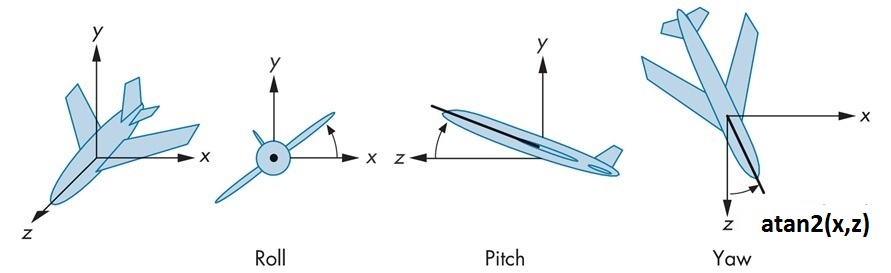
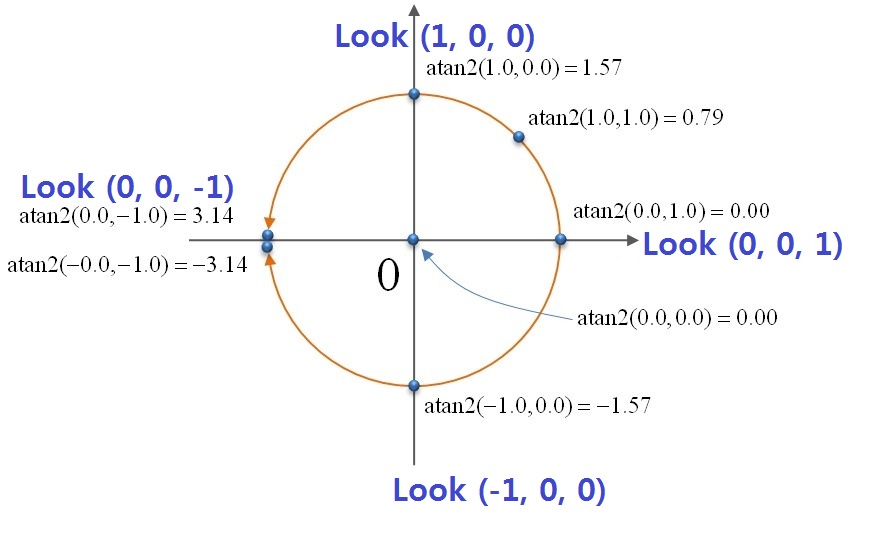
// create a axis-aligned billboard matrix
void buildAxisAlignedBillboardMatrix(glm::mat4& m, glm::vec3& axis)
{
// calculate “-yaw” angle from View matrix (Look.x, Look.z)
float theta = -atan2f(m[0][2], m[2][2]);

float ct = cosf(theta);
float st = sinf(theta);

// normalize
axis = glm::normalize(axis);

// clear out the view matrix passed in
m = glm::mat4(1.0f);

//———————————————
// R = uu’ + cos(theta)*(I-uu’) + sin(theta)*S
//
// S = 0 -z y u’ = (x, y, z)
// z 0 -x
// -y x 0
//———————————————
// calculate “Rotation” matrix using “axis” & “theta”
m[0][0] = axis[0] * axis[0] + ct*(1 – axis[0] * axis[0]) ;
m[0][1] = axis[0] * axis[1] + ct*(0 – axis[0] * axis[1]) + st*(-axis[2]);
m[0][2] = axis[0] * axis[2] + ct*(0 – axis[0] * axis[2]) + st*axis[1];

m[1][0] = axis[1] * axis[0] + ct*(0 – axis[1] * axis[0]) + st*axis[2];
m[1][1] = axis[1] * axis[1] + ct*(1 – axis[1] * axis[1]) ;
m[1][2] = axis[1] * axis[2] + ct*(0 – axis[1] * axis[2]) + st*(-axis[0]);

m[2][0] = axis[2] * axis[0] + ct*(0 – axis[2] * axis[0]) + st*(-axis[1]);
m[2][1] = axis[2] * axis[1] + ct*(0 – axis[2] * axis[1]) + st*axis[0];
m[2][2] = axis[2] * axis[2] + ct*(1 – axis[2] * axis[2]) ;
}

Billboard가 활성화가 되지 않은 상태 (카메라의 시점이 회전된 상태에 따라 알파텍스쳐 나무가 원래 위치한대로 그대로 유지함)

 

Billboard가 활성화된 상태 (카메라의 시점이 회전된 상태라 해도 알파텍스쳐 나무가 내 시점을 향하여 바라보는 상태를 유지함)

 

Blending filter

lab16-BlendFilterTextureShadedQuad

glEnable(GL_BLEND);
if (g_filter == 0) // Default (no blending) = Cs*1
glBlendFunc(GL_ONE, GL_ZERO);
else if (g_filter == 1) // Draw background only = Cd*1
glBlendFunc(GL_ZERO, GL_ONE);
else if (g_filter == 2) // Cs*1 + Cd*1
glBlendFunc(GL_ONE, GL_ONE);
else if (g_filter == 3) // Alpha blending (back-to-front) = Cs*As + Cd*(1-As)
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
else if (g_filter == 4) // brighten the scene = Cs*As + Cd*1
glBlendFunc(GL_SRC_ALPHA, GL_ONE);
else if (g_filter == 5) // Modulate blending = Cd*Cs
glBlendFunc(GL_ZERO, GL_SRC_COLOR);
else if (g_filter == 6) // darken the scene = Cd*As
glBlendFunc(GL_ZERO, GL_SRC_ALPHA);
else if (g_filter == 7) // Invert all the colors = Cs*(1-Cd)
glBlendFunc(GL_ONE_MINUS_DST_COLOR, GL_ZERO);
Default (no blending)

Draw background only

Add blending

Alpha blending

Brighten the scene

Modulate blending

Darken the scene

Invert all the colors

Alpha Blending Texture & Fader

lab16-AlphaBlendFaderTextureShadedQuad

Single-Pass Multi-texturing (using multitexQuad defining texCoord0 & texCoord1 & )

lab15-SinglepassMultiTexturing

Multi-Pass Multi-texturing (draw Quad twice using add/modulate blending filter)

lab15-MultipassMultiTexturing

Add Blending (덧셈 블렌딩)

Modulate Blending (곱셈 블렌딩)

lab14-TextureShadedQuad-FilteringWrappingAnimation

animatedTexture (flipbook animation)

texture filtering
// LL mag nearest – min nearest
// LR mag linear – min linear
// UL mag linear – min linear – mipmap nearest
// UR mag linear – min linear – mipmap linear

texture wrapping – texCoords LL(-1, -1), LR(3, -1), UL(-1, 3), UR(3, 3)
// LL CLAMP
// LR CLAMP_TO_EDGE
// UL REPEAT
// UR MIRRORED_REPEAT

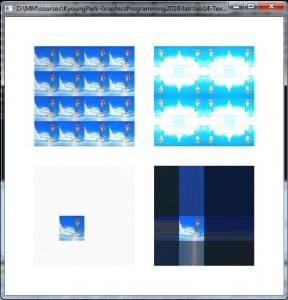
lab13-TextureShadedGeometry-Pyramid

Texture2D 클래스 사용한 Texture Mapping 정의

GeometryPositionNormalTexture 클래스 사용

‘g’-key 사용, Texture Pyramid->Cube->Sphere->Cylinder->Torus->Parallelepiped->Grid 변환

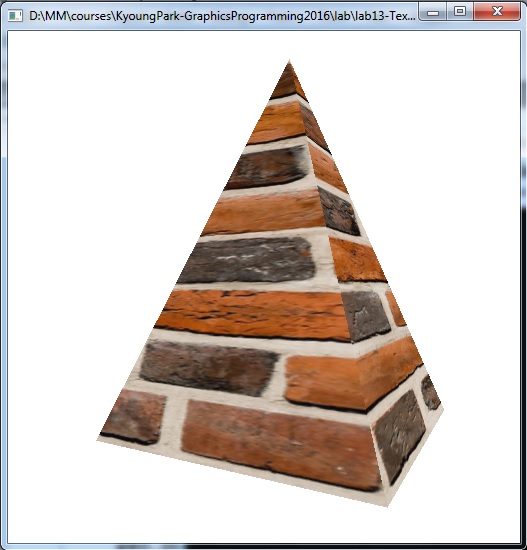
void Cone::init()
{
numVertices = 0;
glm::vec3 n(0.0f, 0.0f, 0.0f);
float xTexCoord = 0.0f;
float dslice = 1.0f / slices;

float theta = (float)(2 * M_PI / slices);
for (int i = 0; i < slices; i++)
{
glm::vec3 v1, v2, v3;
// V1
v1[0] = p[0];
v1[1] = p[1] + height;
v1[2] = p[2];
// V2
v2[0] = p[0] + radius * cosf(theta * i);
v2[1] = p[1];
v2[2] = p[2] + radius * sinf(theta * i);
// V3
v3[0] = p[0] + radius * cosf(theta * ((i + 1) % slices));
v3[1] = p[1];
v3[2] = p[2] + radius * sinf(theta * ((i + 1) % slices));
// Normal
glm::vec3 n = glm::cross((v2-v1), (v3-v1));
n = glm::normalize(n);
printf(“V1: %f %f %f\n”, v1[0], v1[1], v1[2]);
printf(“V2: %f %f %f\n”, v2[0], v2[1], v2[2]);
printf(“V3: %f %f %f\n”, v3[0], v3[1], v3[2]);
printf(“N: %f %f %f\n\n”, n[0], n[1], n[2]);

// V1
vbo.addData(&v1, sizeof(glm::vec3)); // vertex position
vbo.addData(&glm::vec2(xTexCoord + dslice * 0.5f, 1.0f), sizeof(glm::vec2)); // vertex texture coordnate (TopCenter)
vbo.addData(&n, sizeof(glm::vec3)); // vertex normal
// V2
vbo.addData(&v2, sizeof(glm::vec3)); // vertex position
vbo.addData(&glm::vec2(xTexCoord, 0.0f), sizeof(glm::vec2)); // vertex texture coordnate
vbo.addData(&n, sizeof(glm::vec3)); // vertex normal
// V3
vbo.addData(&v3, sizeof(glm::vec3)); // vertex position
vbo.addData(&glm::vec2(xTexCoord + dslice, 0.0f), sizeof(glm::vec2)); // vertex texture coordnate
vbo.addData(&n, sizeof(glm::vec3)); // vertex normal

xTexCoord += dslice; // increment texCoord
numVertices += 3;
}

createVAO();
isLoaded = true;
}

GLSL built-in variables gl_Vertex, gl_Normal, gl_MultiTexCoord0 (version 130 까지만 지원)

GLSL Tutorial

https://www.opengl.org/sdk/docs/tutorials/TyphoonLabs/Chapter_3.pdf

Light & Material를 사용하여 glutTeapot, glutSolidSphere, glutSolidCylinder를 Shading

lab12-ShadedGLUT

Light & Material & Texture를 사용하여 glutTeapot, gluSphere, gluCylinder를 Shading

lab12-TextureShadedGLUT

simage
COIN3D simage library (http://www.coin3d.org/lib/simage)

• • COIN3D simage가 제공하는 이미지 포멧은 JPEG, PNG, GIF, TIFF, RGB, PIC, TGA, EPS등 다양하다.
  • COIN3D의 simage library를 사용하려면, 프로젝트에 additional library and include directory를 추가해야한다. 기존 include 와 lib 디렉토리 안에 simage.h 과 simage1d.lib를 복사한다.
  • 그리고, 텍스쳐 이미지 로딩을 위해 프로젝트에 simage1.lib 라이브러리를 링크한다.